
Greeting: Welcome to my Web page! Please come to see me!
I’m Nakamura, a Japanese geometric quilt designer. It has been serialized in BP&Q magazine since last year, so I think some of you may have seen it.
I will join FOQ for the first time and will talk about how to use PowerPoint to create original geometric quilt designs.
In the lecture, I concretely propose a method to create an original geometric pattern, and make it easy to realize using PowerPoint.
And since the PowerPoint file based on that methodology can be downloaded for free, you can try the proposed method. Please try to make your original geometric quilt design!
The first key to the methodology is to use a combination of polygons instead of a square grid when creating a quilt design.
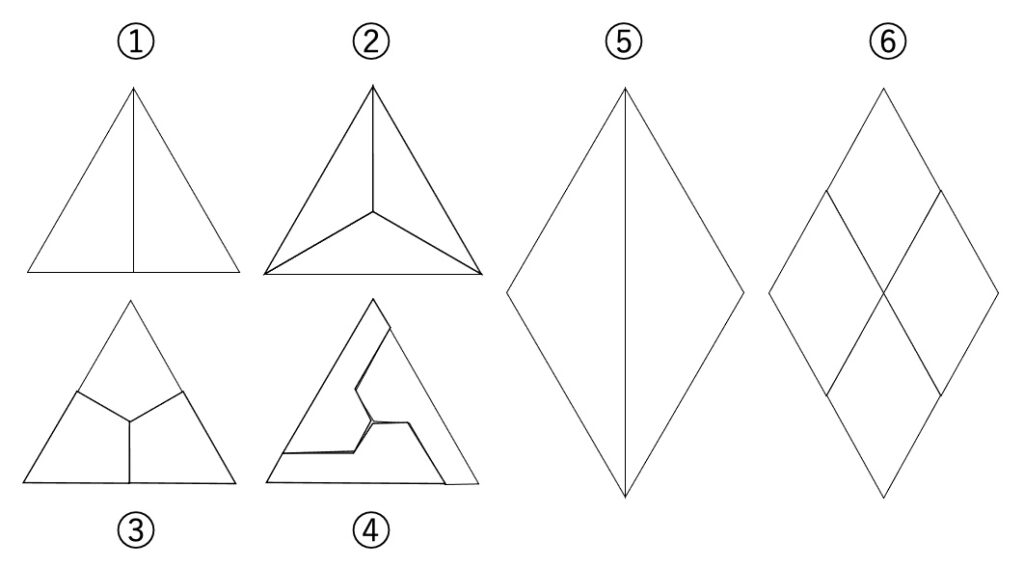
The second key to the methodology is to use internal dividing. The following video explains the contents very briefly. If you find it interesting, please join to the lecture as there is also a coupon for the lecture. Also I have a booth, so I am looking forward to seeing you then.
Free pair ticket for FOQ: Send me Email Soon!
I get the digital code of the pair ticket from FOQ office. If you want it. Please Email me at the following address.
Email address: col.kenzou.nakamura@kenzonakamura
My Booth: D45 Please come to see me!
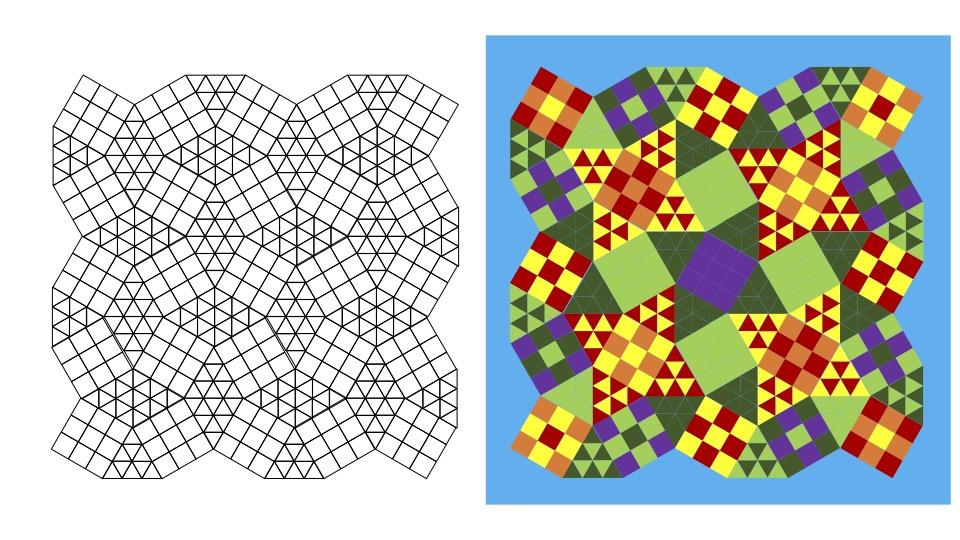
I will exhibit my original geometric design quilt. Following is the Main Quilt “Galaxy”.

If you want to make an original geometric design quilt, please come to see me!.

Coupon Code: Please join my lecture!
This coupon is used when applying for a lecture. 2 pounds discount.
Coupon Code: WT22
- How to Join the lecture
- 1. Go to the Web of FOQ booking page(below).
- 2. Enter “kenzo” in selecting row.
- 3. Select the course. ※The two courses have the same contents.
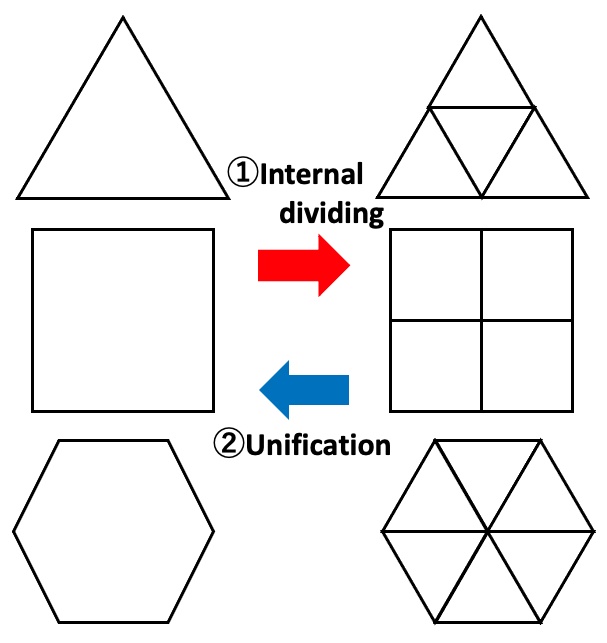
What is the Internal Dividing?
- Geometric Internal Dividing
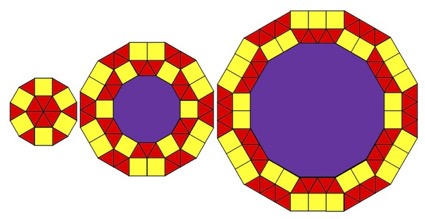
2. Internal Dividing with a hierarchical structure of regular dodecagons
3. Repeating Internal Dividing
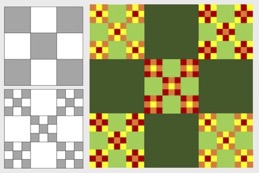
4. Internal Dividing on design
For more detail, read the following reference book.


