要約:Mathematica グラフィックス入門となる円と円盤のグラフィックス・プリミティブCircleとDiskについて解説する。
円・円板を表わすグラフィクス・プリミティブ
グラフィクス・プリミティブCircle[]とDisk[]を使い、円による幾何学模様を描いてみたい。
Circle[]は線で円を描く命令であり、Disk[]は、円の中を塗りつぶす、いわば円板である。図1にあるように普通の円であれば、Circle[{x,y},r]の形で中心と半径を与えればよい。更に円弧または扇形を描きたいのであれば描き初めと描き終りの角度を加えて、Circle[{x,y},r,{T1,T2}]の形にする。この時、T1<T2である必要がある。これは時計周りと反時計周りの2つの扇ができることを防ぐためである。
また、楕円であればx、y方向の半径を与えて、Circle[{x,y},{Rx,Ry}]の形で命令を書けばよい。当然、Circle[{x,y},{Rx,Ry},{T1,T2}]の形で楕円の扇も描くことができる。但し、軸が傾いた楕円を描くことはできない。
なお、2つの命令の使い方はほぼ同じであるので、可能なものについては、この両者を平行して使用し、図を描いてみることにする。
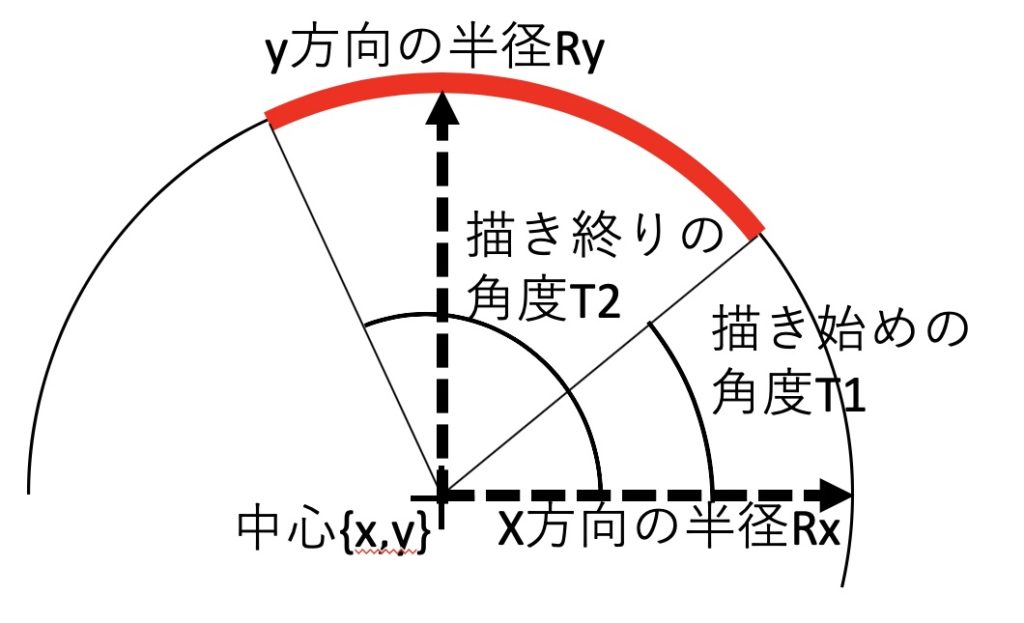
図1:Circle[]とDisk[]の使い方の説明
1.5.1 同心円とその重なり
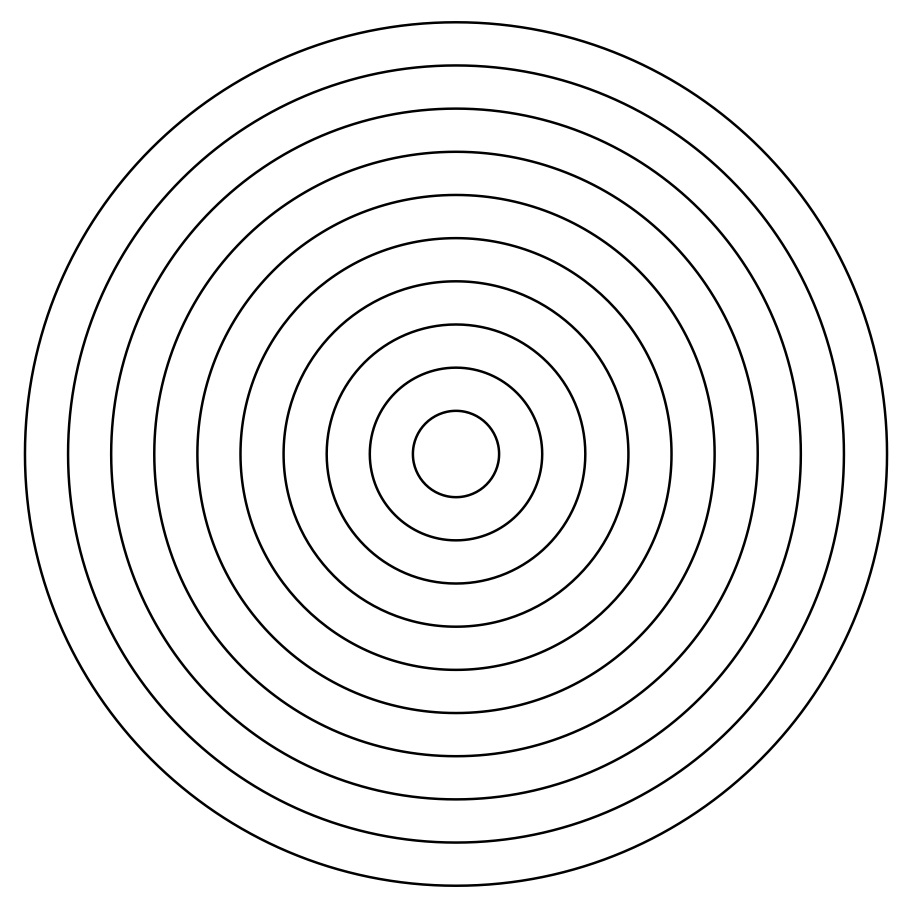
中心を同じくする円の半径を規則正しく変更して描いたものが、図2及び図3の同心円である。
図2:同心円 図3:同心円(陰影)
<<プログラム1>>
Show[Graphics[Table[Circle[{0,0},i],
{i,1,10}]],AspectRatio->1];(*図2*)
Show[Graphics[Evaluate[Table[{GrayLevel[Mod[i,11]/10],
Disk[{0,0},i]},{i,10,1,-1}]]],AspectRatio->1];(*図3*)
プログラム1では、半径を10~1まで1ずつ小さくしながら、円を描いている。
図2の同心円を3つ重ねたものが図3の図である。

図4:マーブル(大理石)模様
<<プログラム2>>
Show[Graphics[Table[{Hue [1-Mod[i,11]/10],
Disk[{-2,0},i],Disk[{2,0},i],Disk[{0,2},i]},{i,20,2,-1}]],
AspectRatio->Automatic](*図4*)
プログラム2では3つの同じ半径の円を半径を小さくしながら描いている。
円の重なり
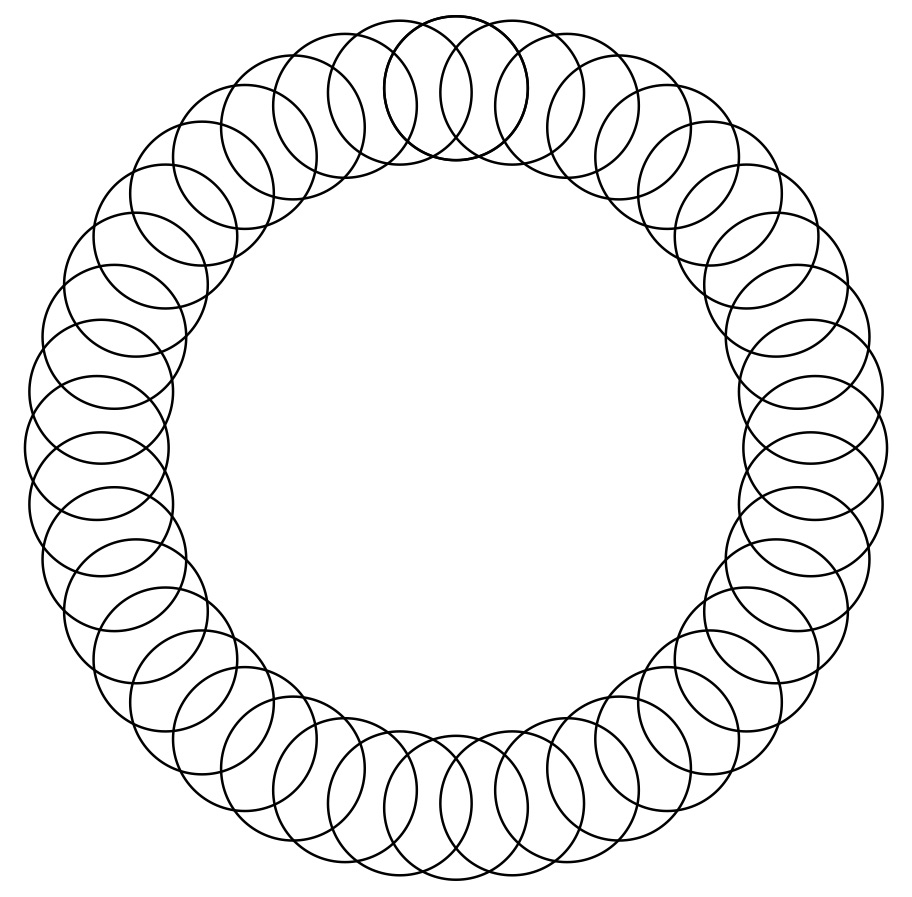
円の中心を同じにするのではなく、中心位置を規則正しく変化させたものが、図5~図12である。
図5:円の重なり
<<プログラム3>>
Show[Graphics[Table[
Circle[{i,0},i],{i,1,10}]],AspectRatio->1];(*図5左*)
Show[Graphics[Evaluate[Table[{Hue[i/10],
Disk[{i,0},i]},{i,10,1,-1}]]],AspectRatio->1];(*図5右*)
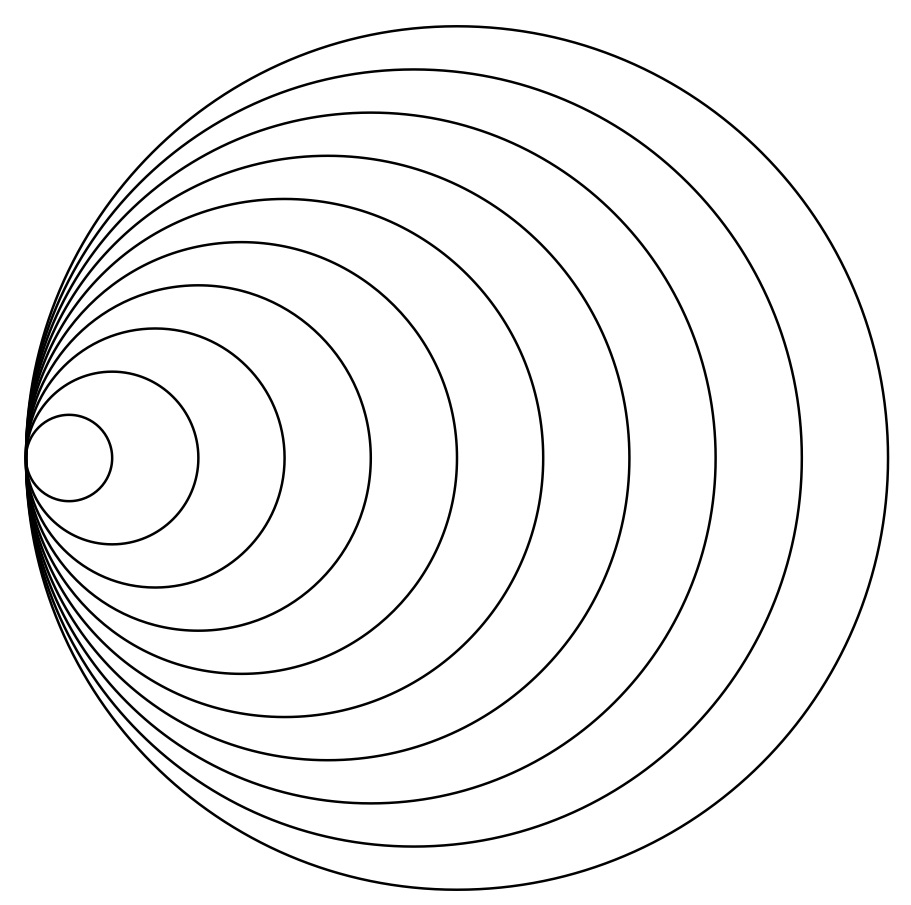
図5のプログラムでは、半径と中心のx座標を同じにすることで、円周の1点が接した円群を描いている。
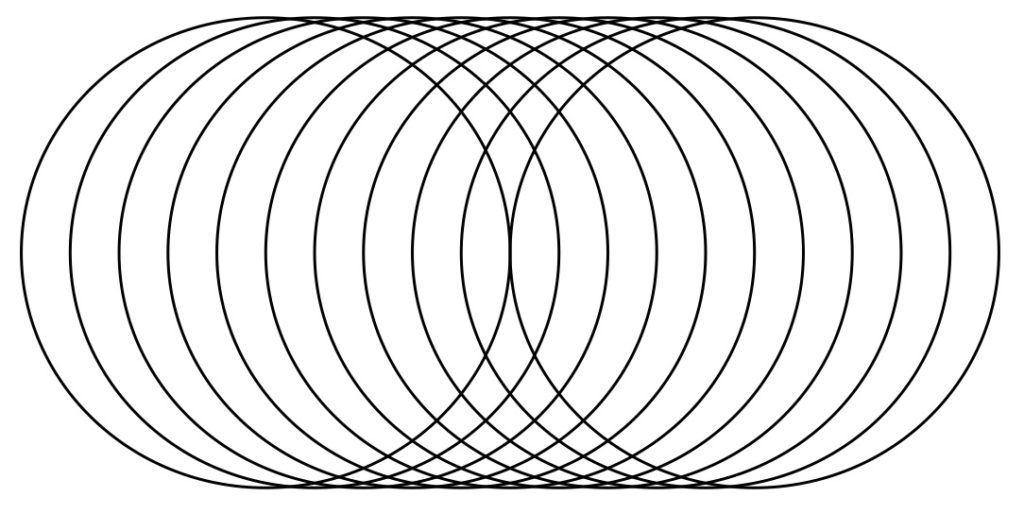
図6:円の重なり(その2:平行移動)
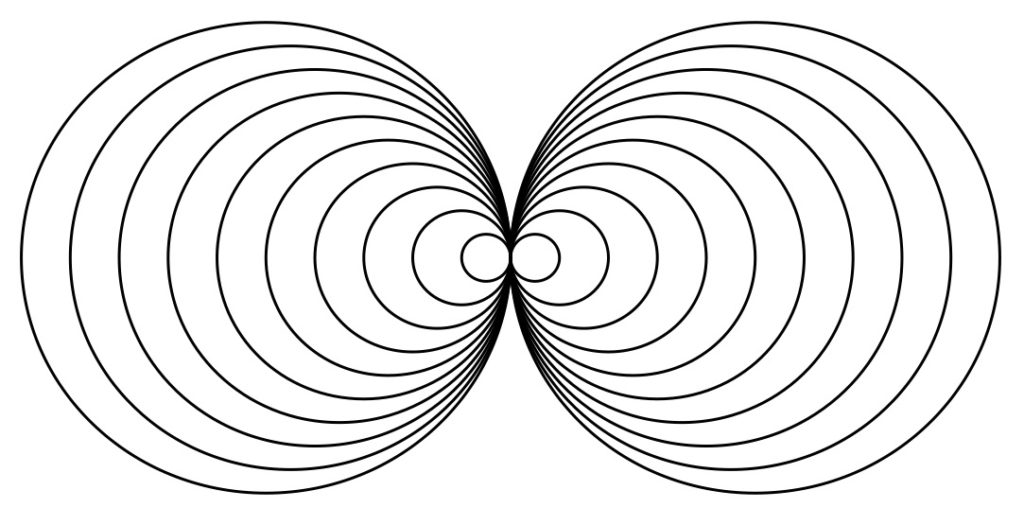
図7:円の重なり(その3:向い合わせ)
<<プログラム4>>
Show[Graphics[Table[
Circle[{i,0},5],{i,0,10}]],AspectRatio->0.5];(*図6*)
a=Table[Circle[{i,0},Abs[10-i]],{i,0,20}];
Show[Graphics[a],AspectRatio->0.5](*図7*)
図6のプログラムでは、半径一定で中心のx座標だけを変化させている。また、図7では、円の中心を0~20まで動かしながら半径をAbs[10-i]の形で10~0まで減らし、その後また10まで増やすことで向かい合わせの円を1つの式で実現している。
図8:円の重なり(その4:向い合わせ)
<<プログラム5>>
a=Table[Circle[{i,0},10-Abs[i]],{i,-10,10}];
Show[Graphics[a],AspectRatio->1];(*図8左*)
a=Table[{GrayLevel[Mod[i,11]/10],Disk[{i,0},10-i],
Disk[{-i,0},10-i]},{i,0,9}];
Show[Graphics[a],AspectRatio->1];(*図8右*)
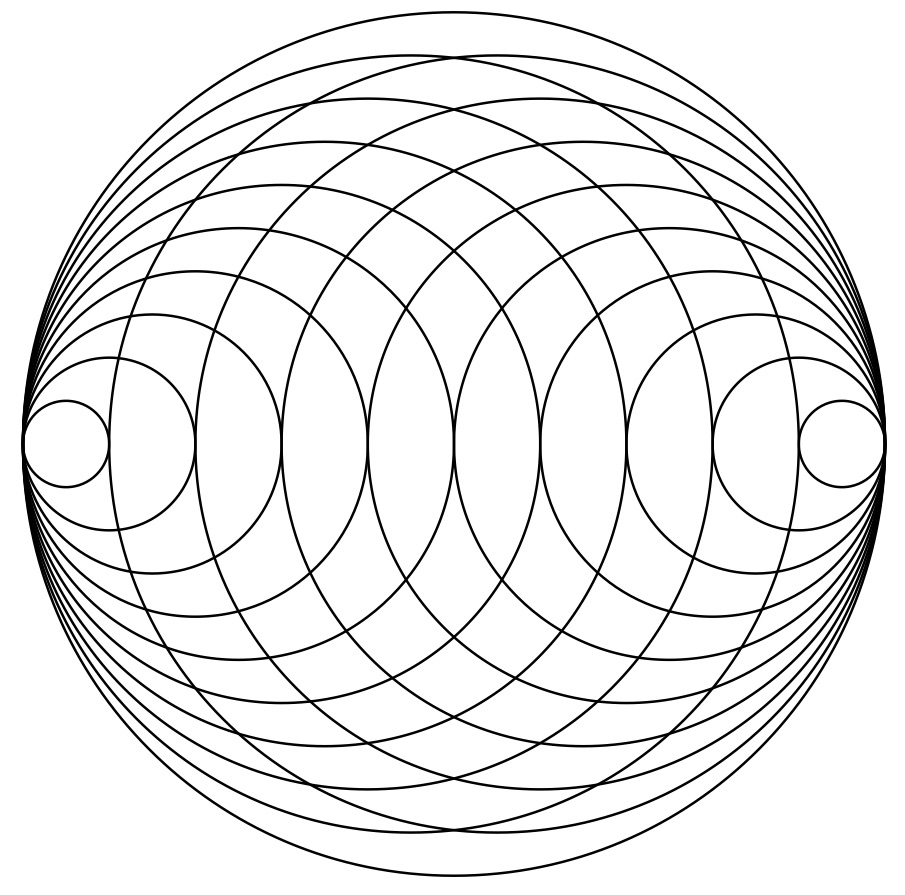
図8左のプログラムでは、円の中心をー10~10まで動かしながら半径を10-Abs[i]の形で0~10まで増加させ、その後また0まで減らすことで向かい合わせの円を1つの式で実現している。
図8右のプログラムでは、左と同じにすればいいように思えるが、同じ半径の2つの円を大きいほうから描いているのである。
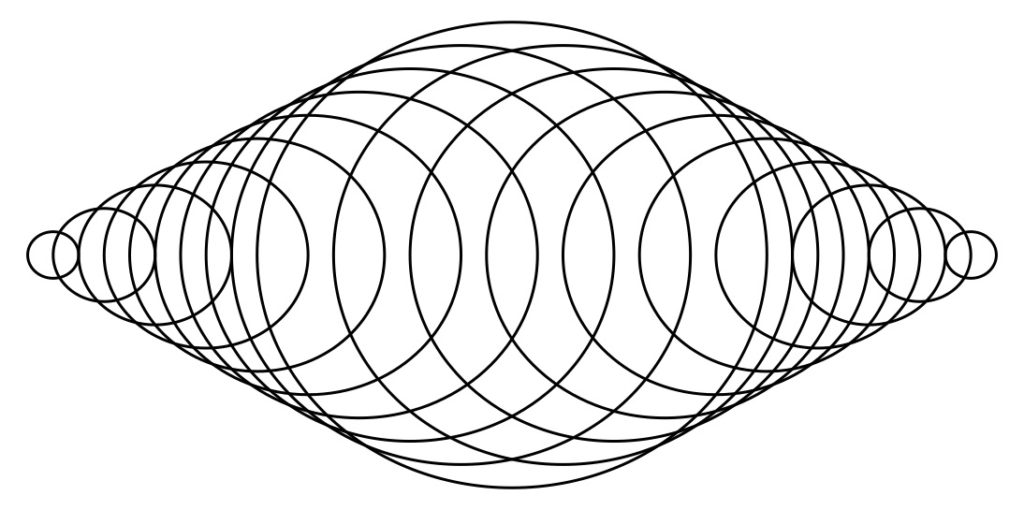
図9:円の重なり(その5:向かい合わせ)
<<プログラム6>>
a=Table[Circle[{i,0},5-Abs[i]/2],{i,-9,9}];
Show[Graphics[a],AspectRatio->.5]
図9のプログラムは、図8左のプログラムとほぼ同じであるが、半径の増加分よりも中心の移動量を多くずらしている。
図10:円の重なり(その6) 図11:円の重なり(その7)
<<プログラム7>>
a=Table[{GrayLevel[Mod[i,11]/10],Disk[{i,0},10-i],Disk[{-i,0},10-i],
Disk[{0,i},10-i],Disk[{0,-i},10-i]},{i,0,9}];
Show[Graphics[a],AspectRatio->1];(*図10*)
a=Table[{GrayLevel[Mod[i,11]/10],
Disk[{2*i,2*i},10-i],Disk[{-2*i,-2*i},10-i],
Disk[{-2*i,2*i},10-i],Disk[{2*i,-2*i},10-i]},{i,0,9}];
Show[Graphics[a],AspectRatio->1](*図11*)
図10のプログラムは、同時に4つの円を描いている。また、図11も同じであるが、x,y方向に同じ量だけずらすことで、斜め方向への移動を行っている。
図12:円の重なり(その8)
<<プログラム8>>
Show[Graphics[Evaluate[Table[Circle[{Sin[i/5],Sin[i/5]},i/3],
{i,30,1,-1}]]],AspectRatio->1];
Show[Graphics[Evaluate[Table[{Hue[1-Mod[i,11]/10],
Disk[{Sin[i/5],Cos[i/5]},i/7]},{i,70,1,-1}]]],AspectRatio->1];
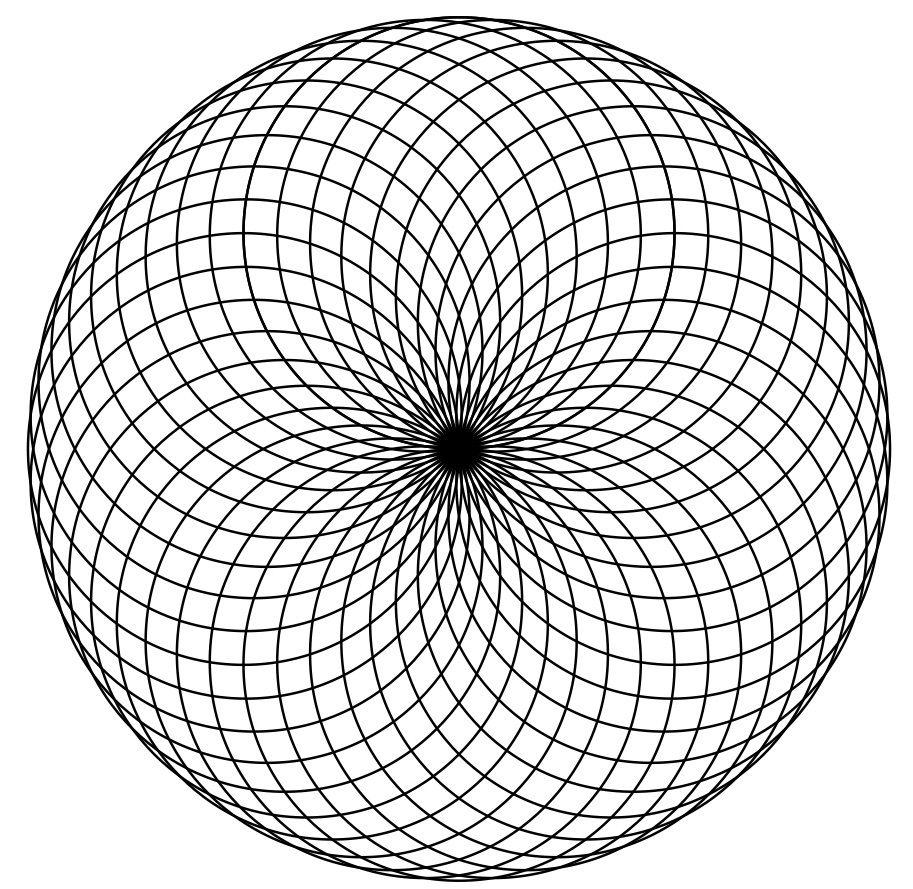
図12は、螺旋状に小さくなっているように見えるが、プログラムで分かるように円の中心を単位円上で回転させながら、半径を小さくしているのである。
図13:円の重なり(その9) 図14:円の重なり(その10)
<<プログラム9>>
a=Table[Circle[{Sin[t],Cos[t]},1],{t,0,2Pi,Pi/20}];
Show[Graphics[a],AspectRatio->1];(*図13*)
b=Table[Circle[{Sin[t],Cos[t]},.2],{t,0,2Pi,Pi/20}];
Show[Graphics[b],AspectRatio->1](*図14*)
図13のプログラムでも図12と同じように、円の中心を単位円上で回転させながら円を描いているのであるが、円の半径が1で一定であることが大きく異なることである。また、図14も同じであるが、中心の回転半径が円自体の半径よりも大きくなっている点が異なる。
円の重なりだけでも、いろいろなバリエーションを考えることができる。他のパターンについても、いろいろ考えられるので挑戦していただきたい。
楕円
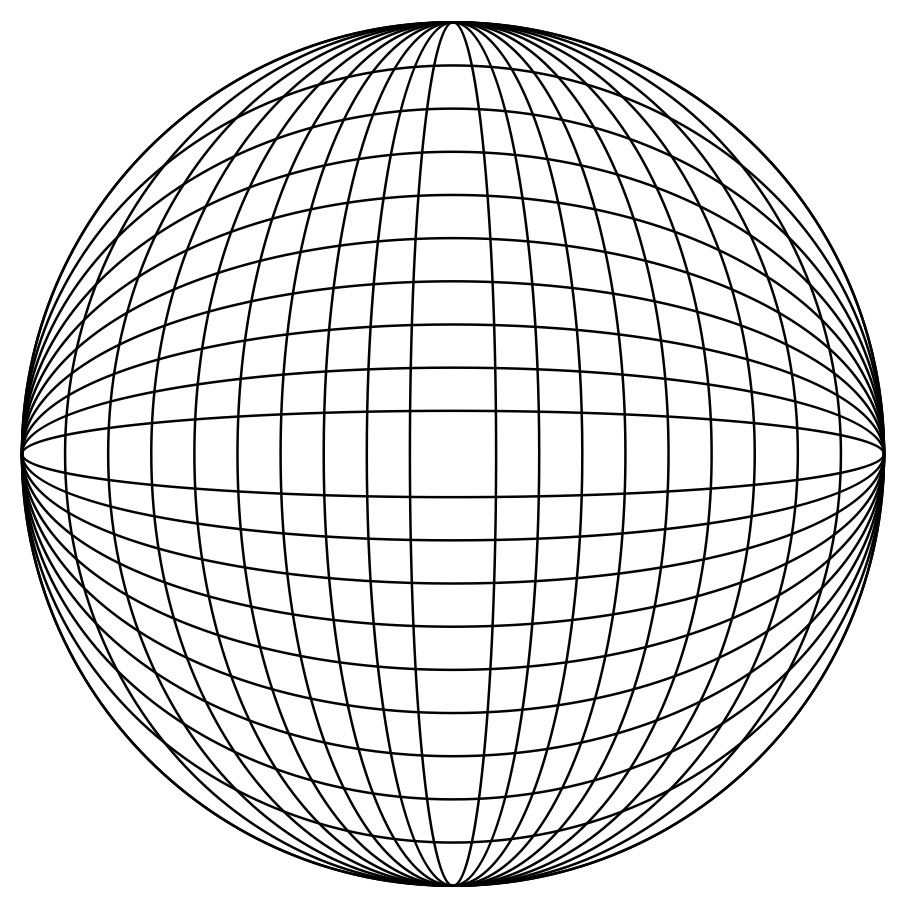
楕円はCircle[{x,y},{Rx,Ry}]の形式で中心座標以外にx、y方向の半径{Rx,Ry}を代入することで描くことができる。楕円による幾何学的な構成を図15~図17に示す。
図15:楕円の重なり(その1)
<<プログラム10>>
a=Table[Circle[{0,0},{10,i}],{i,1,10}];
b=Table[Circle[{0,0},{i,10}],{i,1,10}];
Show[Graphics[{a,b}],AspectRatio->1];(*図15左*)
a=Table[{GrayLevel[Mod[i,11]/10],Disk[{0,0},{10,11-i}],
Disk[{0,0},{11-i,10}]},{i,1,10}];
Show[Graphics[a],AspectRatio->1](*図16右*)
図15右のプログラムでは、だんだん細くなる順番で2つの楕円を同時に描いている。
図16:楕円の重なり(その2)
<<プログラム11>>
c=Table[Circle[{0,0},{i,3}],{i,1,10}];
d=Table[Circle[{0,0},{3,i}],{i,1,10}];
Show[Graphics[{c,d}],AspectRatio->1];(*図16左*)
a=Table[{GrayLevel[1-Mod[i,11]/10],Disk[{0,0},{11-i,3}],
Disk[{0,0},{3,11-i}]},{i,1,10}];
Show[Graphics[a],AspectRatio->Automatic](*図16右*)
図16では楕円のx、y軸の一方を3に固定し、もう片方を1~10まで変化させている。

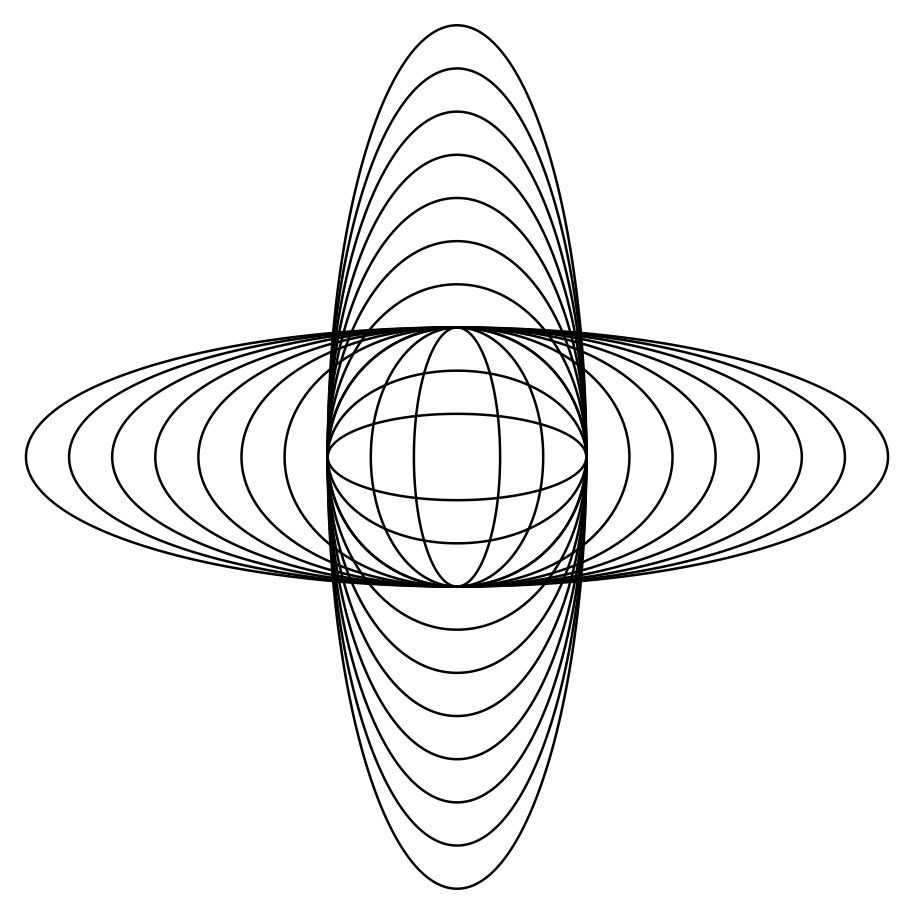
図17:楕円の重なり(その3)
<<プログラム12>>
a=Table[{Hue[1-Mod[i,11]/10],Disk[{i-i/3,0},{i,3+i/2}]},{i,15,1,-1}];
Show[Graphics[a],AspectRatio->Automatic]
図17では、縦横の長さをそれぞれ変えながら、小さい楕円が消されないように、また、外にはみ出さないように中心を移動させて描いている。
扇形を使った図形
Circle[{x,y},r,{T1,T2}]の形式で角度{T1,T2}を指定することで、扇形を描くことができる。同じ円の中心で、半径、扇の角度及び陰影を変化させたものが図47である。

図18:同心の扇形
<<プログラム13>>
a=Table[{GrayLevel[Mod[i/20,1]],
Disk[{0,0},1-i/20,{i*Pi/40,Pi(1-i/40)}]},{i,1,20}];
Show[Graphics[a],AspectRatio->Automatic]
プログラム13では、iを1~20として1/20刻みでグラジュエーションを作図している。
次は、半円を使い、円の中心は一致しているが、位置が異なるものと昔のTVゲームであったパックマンを思い出させる扇形を使い、中心を変えながら並べた例を上げる。
図19:半円のくい違い 図20:パックマンの逆襲
<<プログラム14>>
a=Table[{GrayLevel[Mod[i/20,1]],
Disk[{0,0},1-i/20,{Pi*i/2,Pi(1+i/2)}]},{i,1,20}];
Show[Graphics[a],AspectRatio->Automatic](*図19*)
a=Table[{GrayLevel[Mod[i*j/16,1]],
Disk[{i,j},0.45,{Pi((i+j)/2-1/3),Pi((i+j)/2+4/3)}]},{i,1,4},{j,1,4}];
Show[Graphics[a],AspectRatio->Automatic](*図20*)
図19のプログラムでは、半円の角度を反時計周りに90度ずつずらしている。
図20では、中心を{i,j}としてi+jをうまく使うことで、その座標ごとに扇の角度を変えている。
扇形を利用して描ける幾何学図形として大極と呼ばれものがある。

図21:韓国国旗の真ん中にある模様
<<プログラム14>>
Show[Graphics[{Table[{GrayLevel[Mod[t/(2Pi),1]],
Disk[{0,0},1,{t,t+Pi}]},{t,0,2Pi,Pi}],
Table[{GrayLevel[Mod[(t-Pi)/(2Pi),1]],
Disk[0.5*{Cos[t],Sin[t]},0.5,{t-0.01,t+Pi}]},{t,0,2Pi,Pi}]}],
AspectRatio->Automatic]
図21は、カラーではないが、韓国国旗の真ん中にある模様で、これは大極と呼ばれ、陰陽が移り行く様を表わす模様なのだそうである。この模様と同様に円の分割数を3から6まで増やした模様を図22に示す。

図22:分割数2,3,4,5,6の模様
<<プログラム15>>
Table[
Show[Graphics[{Circle[{0,0},1],
Table[Circle[0.5*{Cos[t],Sin[t]},0.5,{t,t+Pi}],
{t,0,2Pi,2Pi/n}]}],AspectRatio->Automatic],{n,2,6}]
なお、分割数3の模様は、韓国オリンピックの時のに使われたものと同じである。円の分割数を5以上に増やすと、塗りつぶすことは出来ないので、分割数3、4で陰影を付けたものが図23である。

図23:分割数2,3,4の模様
<<プログラム16>>
GraphicsRow[Table[Graphics[
{Table[{Hue[Mod[t/(2Pi),1]],Disk[{0,0},1,{t,t+2Pi/n}]}
,{t,0,2Pi,2Pi/n}],
Table[{Hue[Mod[(t-2Pi/n)/(2Pi),1]],Disk[0.5*{Cos[t],Sin[t]},0.5,{t-0.01,t+Pi}]}
,{t,0,2Pi,2Pi/n}]}
,AspectRatio->Automatic],{n,2,4}]]
ところで日本にもよく似た模様で巴(ともえ)というのがある。これは水の流れを表わすものだそうである。
参考文献:Mathematicaグラフィックスの入門書
中村健蔵「Mathematicaで絵を描こう」1997東京電機大学出版局
ノートブックのダウンロード
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。