要旨:MBA取得のためのMathematica 4として待ち行列について解説し、基本的な算定とシミュレーションをMathematicaでできるようにする。
日本のコンビニの平均待ち時間は約40秒と言われている。3人以上待っていると別のコンビニを目指すことが業界では大きな機会損失として重要な課題となっている。では、窓口をいくつ儲ければ良いのかというのが待ち行列である。MBA取得のために基本的なところを学んで頂きたい。
1 全 般
待ち行列は、図1にあるように店などにお客さんが来て、サービスを受けて帰る。この時、お客が連続してきたり、サービスに手間取ったりして客が並ぶ、つまり、買い物やタクシー乗り場で経験したり、見かけたりする行列ができるわけです。この問題を最初に数学的に取り扱ったのは、1900年代の初めにデンマークの電話会社に勤めるアーラン(A.K.Erlang)でした。内容は電話交換の設備の規模をどの程度にすれば経済的かというものであり、人の待ち行列等は現代ほど忙しくないので問題にはならなかったようです。なお、待ち行列と言うと買い物やタクシー乗り場を想像してしまいますが、応用的な例としては電話交換、港の船の積み荷、駐車場、有料道路の料金所、情報ネットワークの設計、並列コンピュータの設計など応用範囲は広くあります。

図1:待ち行列の説明
1.1 簡単な待ち行列のシミュレーション
図1にあるような窓口が1つで、ランダム到着・ランダムサービスの場合の待ち行列の長さの変化をシミュレーションしてみます。なお、ランダム到着・ランダムサービスとは、到着の時間間隔やサービス時間の分布が指数分布に従うような場合をいい、我々が経験するような日常的な待ち行列においては最も自然な時間間隔であると考えられています。
プログラムでは、mm1[平均到着時間、平均サービス時間、シミュレーションの期間]を入力すれば、時間に応じる待ち行列の長さの変化をプロットしてくれます。なお、平均到着時間及び平均サービス時間とは、平均何単位時間で1人の客が到着し、処理できるかということです。
次節では、窓口が1つで、ランダム到着・ランダムサービスの場合の待ち行列について詳しく性質を見てみます。
リスト1にプログラムを、図2から図4にMathematicaの出力結果に説明を加えたものを示しました。
<<リスト1>>
mm1[avt_,ast_,t1_]:=(*関数の定義*)
Module[{q1=0,fq=0,t=0,p1=1./avt,p2=1./ast,a={0} },(*変数の定義*)
While[t<t1,t++;(*t1回まで繰返し*)
If[p1<Random[],q1++,];(*到着*)
If[q1>0 && p2<Random[],q1=q1-1,];(*サービス*)
AppendTo[a,q1] ];(*リストへ出力*)
ListPlot[a,PlotJoined ->True](*作図*)
];
mm1[2.5,3,1000];(*図*)
mm1[3,3,1000];(*図*)
mm1[3.5,3,1000];(*図*)
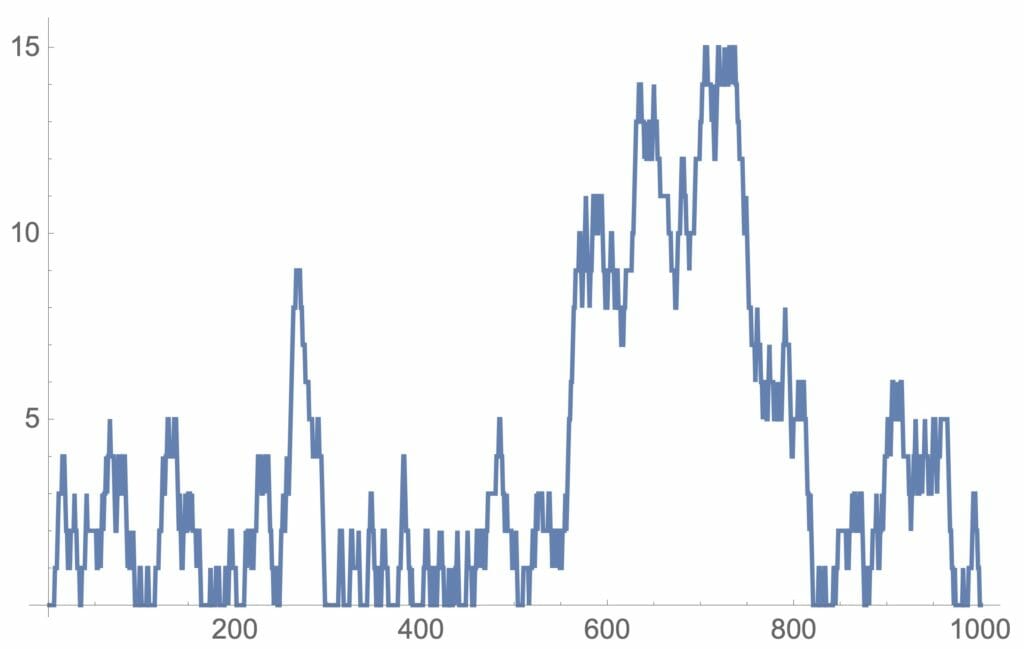
図2:待ち行列の変化(客の到着<サービス)
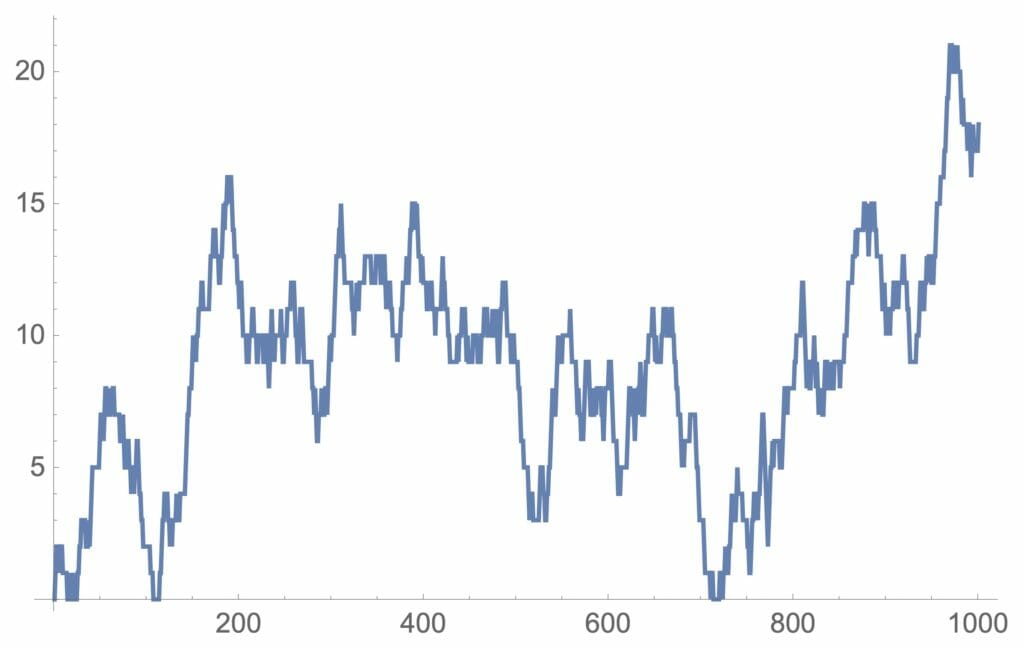
図3:待ち行列の変化(客の到着=サービス)
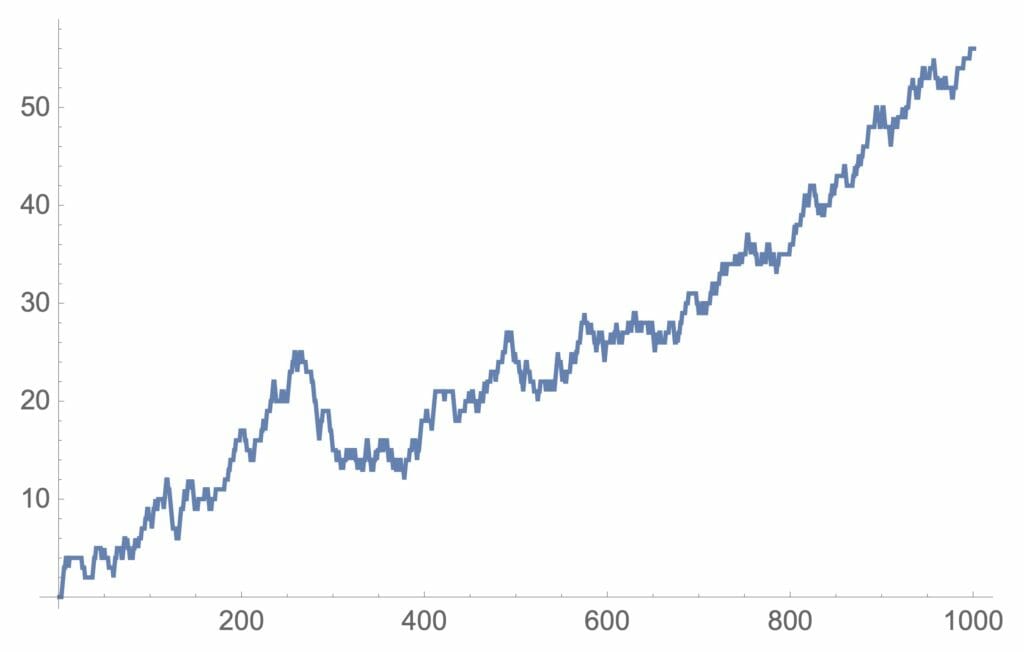
図4:待ち行列の変化(客の到着>サービス)
当然のことですが、図4のように平均サービス時間が平均到着時間より大きい、つまり、サービスが終るより来る客が多い場合には、待ち行列がどんどん大きくなることがよく分かります。図2と図3は、一見同じように見えますが、待ち行列の最大数が26と14であり、平均サービス時間と平均到着時間が等しいときには、待ち行列の最大数が大きいことが分かります。なお、平均サービス時間が平均到着時間より小さな場合でも十分大きな待ち行列ができているということは、繁盛している店には待ち行列がつきものと考えなければならないようです。
1.2 待ち行列の分類(ケンドールの記号)
待ち行列の分類をケンドール(D.G.Kendall)は、M/M/1(N)と表すようにしました。これは、1番目の文字が到着時間の分布、2番目がサービス時間の分布、3番目は窓口の数、最後の括弧の中がサービス中の人を含めて許される待ち行列の最大数を示しています。
分布の記号は
M:指数分布(到着はポアソン到着)
D:レギュラー到着(サービスはサービス時間一定)
G:一般の分布
E:次数kのアーラン分布(ガンマ分布)
などがあります。
なお、ケンドールは英国数学者で、待ち行列の理論的な発展に貢献しました。
2 基本的な待ち行列(M/M/1)
2.1 平衡状態と遷移確率
M/M/1の場合についてマルコフ過程的に待ち行列の状態遷移を図5に示します。
なお、ここでλは平均サービス時間の逆数=サービス率を、μは平均到着時間の逆数=到着率を示しています。これは単位時間当りにサービスが終わる、または、客が到着する確率と考えることができます。したがって、状態遷移を考えるときはこちらで考えることが一般的です。
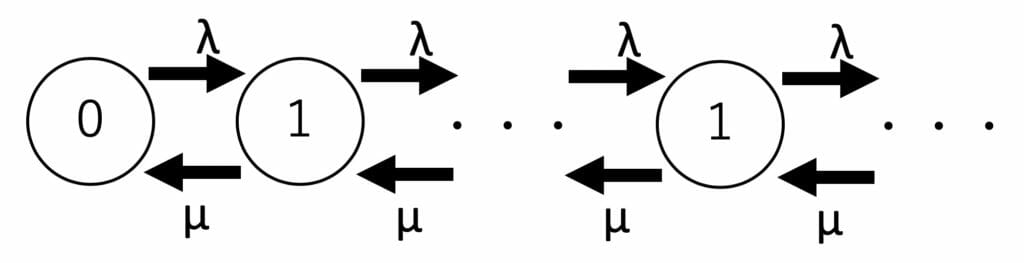
図5:M/M/1の待ち行列の遷移状態
平行状態kにある確率をPkと書くと
λPk-1+μPk+1=(λ+μ)Pk
という式が成り立ちます。但し、λP0=μP1です。
従って、Pkの確率分布は以下の通り求まります。
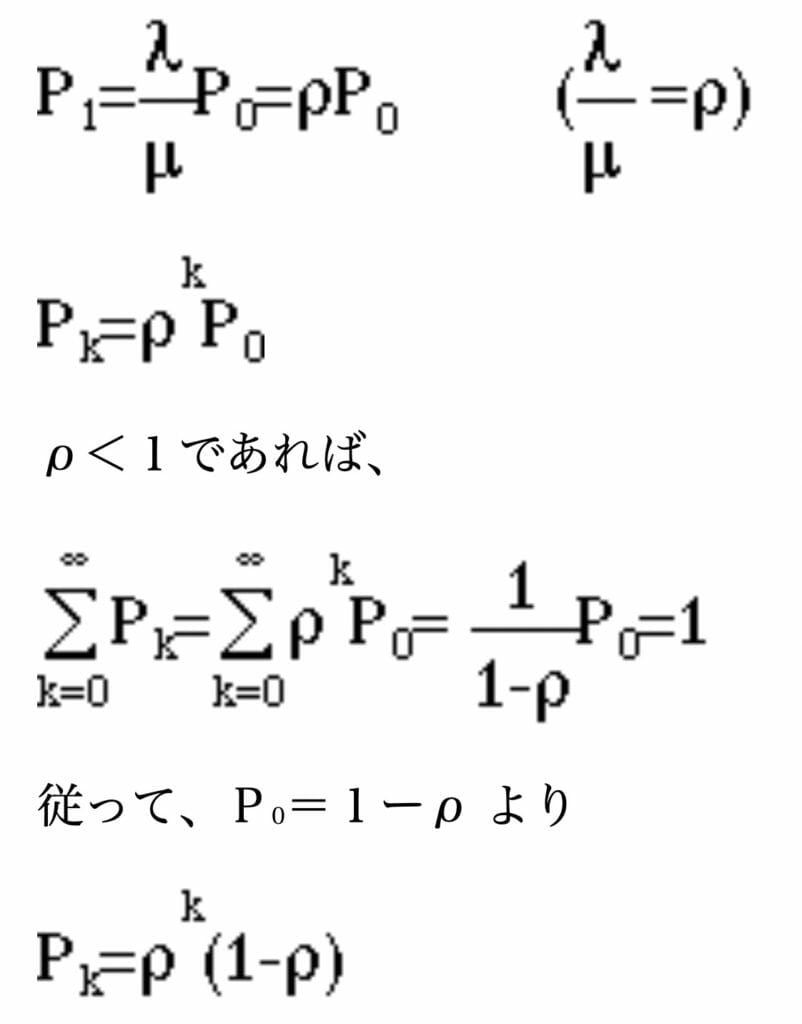
が成り立ちます。
2.2 待ち行列の特性値
(1)利用率
窓口がふさがっている確率は、1ーP0で示されます。これは先程のρの値そのものです。従って、ρのことを利用率といいます。また、トラフィック密度や入量率と呼ぶこともあります。
(2)行列の長さ
系内数(サービス中の人を含める)の平均は、
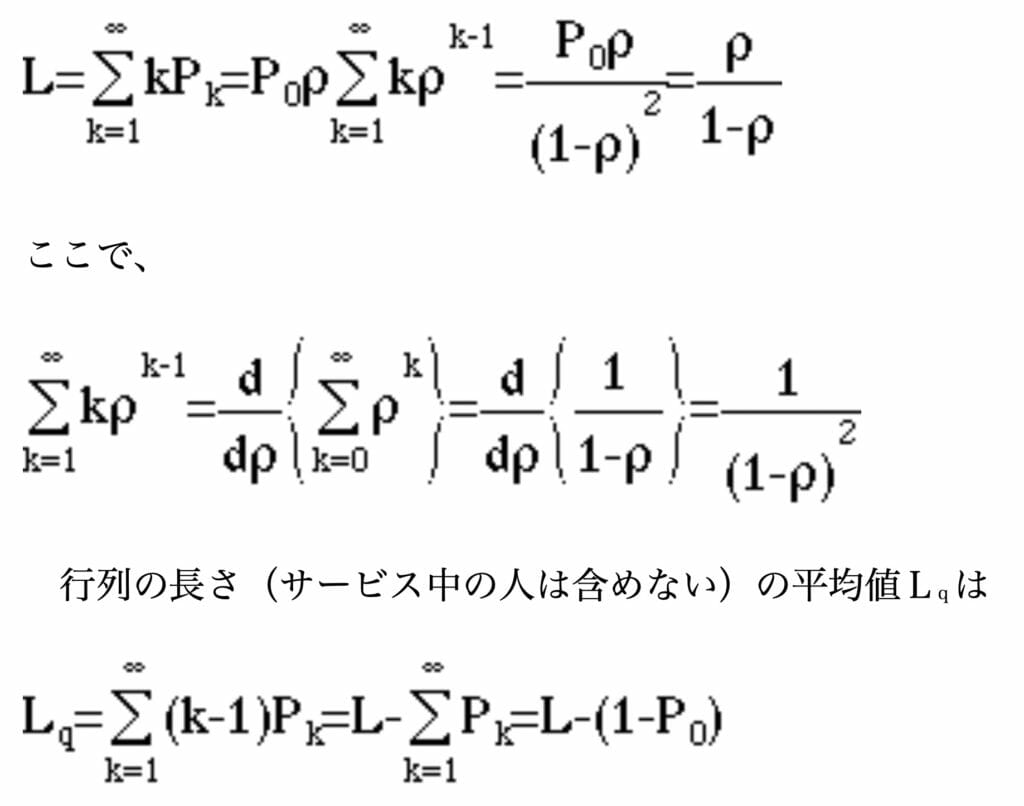
従って、Lq=Lーρの関係があります。
(3)待ち時間
行列の中で待ち時間γがt以上になる分布は次式で示されます。
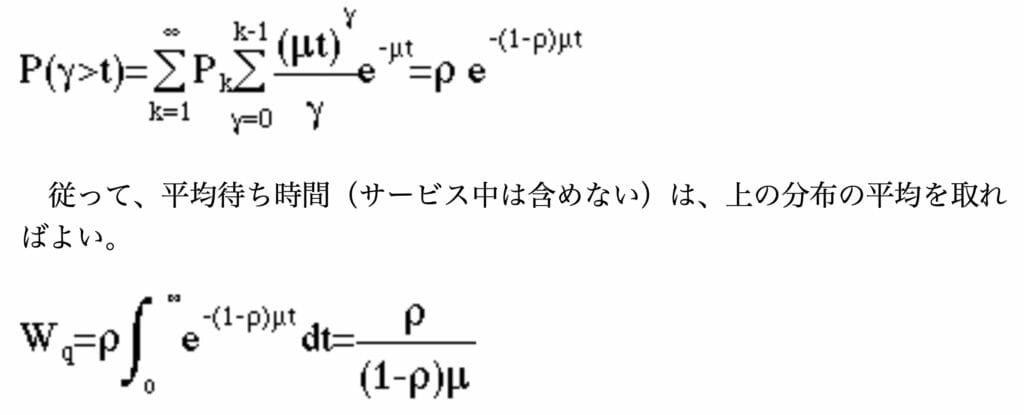
従って、Lq=λWqという関係が成り立ちます。
また、サービスを含めた待ち時間の平均Wは、平均サービス時間の平均と上のWqの和に等しいことは明らかです。
2.3 Mathematicaによる算定
(1)上の結果からM/M/1の特性値をリスト2で算定します。
<<リスト2>>
mm1[mu_,lambda_]:=
Module[{rou=lambda/mu},
Print[“M/M/1の待ち行列“];
Print[“平均サービス時間=“,lambda];
Print[“平均到着時間 =“,mu];
Print[“利 用 率 =“,N[rou]];
If[rou>=1,Print[“ρ≧1で計算不能 “];Break,];
Print[“系 内 数 =“,N[rou/(1-rou)]];
Print[“行列 の 長さ =“,N[rou^2/(1-rou)]];
Print[“滞 在 時 間 =“,N[1/(1-rou)/mu]];
Print[“待 ち 時 間 =“,N[rou/(1-rou)/mu]]]
(*平均サービス時間λ3分、平均到着時間μ4分の系の待ち行列は、*)
mm1[4,3]
M/M/1の待ち行列
平均サービス時間=3
平均到着時間 =4
利 用 率 =0.75
系 内 数 =3.
行列 の 長さ =2.25
滞 在 時 間 =1.
待 ち 時 間 =0.75
(*待ち時間が4分間以上になる確率は、*)
ClearAll[mu, lambda, t, x];
waittime[mu_,lambda_,t_]:=
N[lambda/mu*Integrate[Exp[(lambda-mu)x],{x,t,Infinity}]];
waittime[4,3,4]
0.0137367
(2)シミュレーション
1 全般のところで簡単なシミュレーションを紹介しましたが、そのシミュレーションでは待ち行列の長さの変動を視覚的に把握するためのものでした。ここでは、もう少し精密(イベントシーケンス)に指数分布に従う乱数を使用して、時間等についても厳密な意味でランダム到着・ランダムサービスの待ち行列についてシミュレーションしてみます。 到着時刻と窓口の空く時間の関連を図7に示しました。ここで理解のために重要なものは到着時間間隔から前の客の待ち時間を引いた時間です。これがサービス時間より大きいかどうかで待ち時間があるかどうかを判断できます。さらに図6に関数の流れ図を、リスト3に関数と計算結果を、表1に関数で使用された変数の説明を示しました。
なお、平均到着時間をa、平均サービス時間をbで表すとランダム到着・ランダムサービスの場合の平均待ち時間は、 で表されることが知られています。従って、リスト3の計算例では、平均待ち時間は、0.13333となるはずです。しかしながら、定常状態でないことや有限の平均であることから必ずしも一致していません。
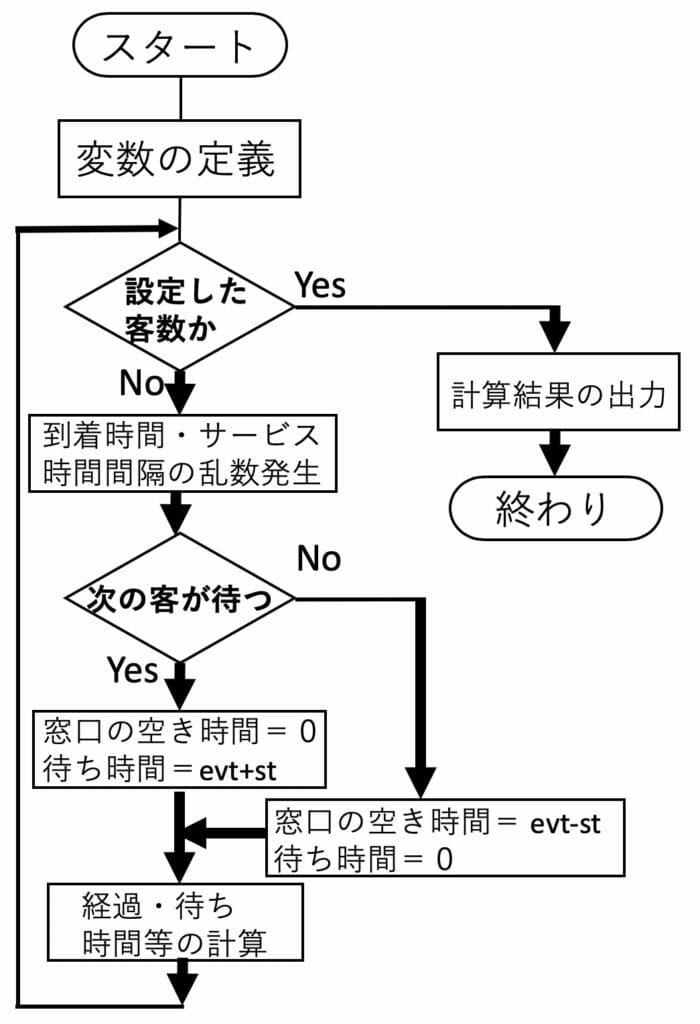
図6:関数singleserverの流れ図
表1:変数の説明
| 関数・変数名 | 意 味 |
| singleserver | 単一窓口モデルの関数名 |
| exrnd | 指数分布に従う乱数を発生させる関数 |
| avt | 平均到着時間 |
| ast | 平均サービス時間 |
| n | シミュレーションしたい客の数 |
| tt | システムの全経過時間 |
| twt | 待ち時間の合計 |
| tidt | 窓口の空き時間の合計 |
| wt | 待ち時間 |
| vt | 乱数で発生させた到着時間 |
| st | 乱数で発生させたサービス時間 |
| evt | 到着時間間隔から前の客の待ち時間を引いたもの |
| idt | 窓口の空き時間 |
- 次の利用者が待つ場合
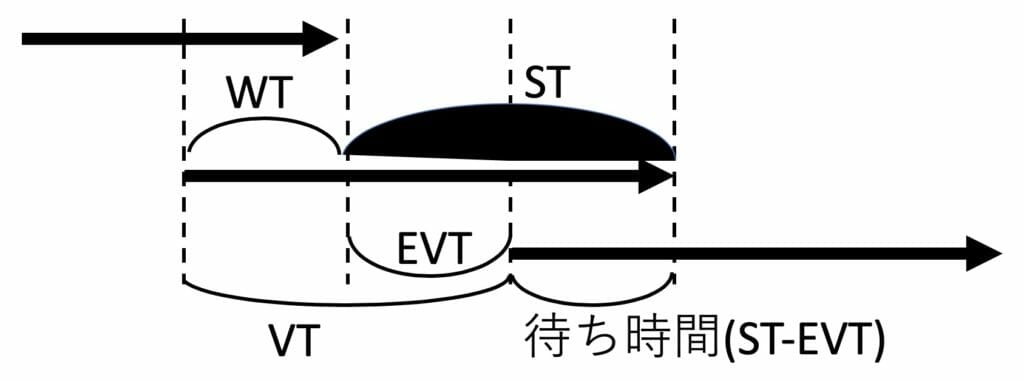
(2)窓口が空く場合(利用者の待ちも窓口の空きもない場合を含む)
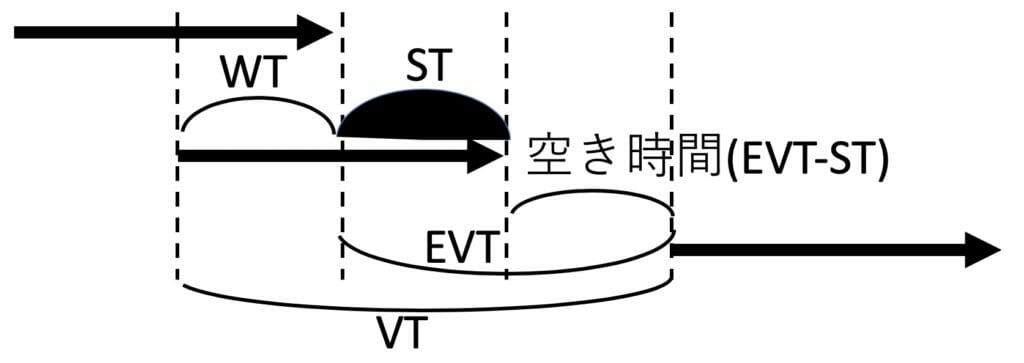
図7:到着時刻と窓口の空く時刻の関連
<<リスト3>>
exrnd[e_]:=-e*Log[Random[]];(*指数分布に従う乱数*)
singleserver[avt_,ast_,n_]:=(*関数の定義*)
Module[{tt=twt=tidt=wt=0,vt,st,evt,idt,},(*変数の定義*)
Do[(*反復*)
vt=exrnd[avt];(*到着時間間隔の乱数発生*)
st=exrnd[ast];(*サービス時間間隔の乱数発生*)
evt=vt-wt;(*到着時間間隔ー待ち時間*)
If[st>evt,idt=0;wt=st+evt,
wt=0;idt=evt-st];(*分岐*)
twt+=wt;(*待ち時間などの計算*)
tt+=st+idt;
tidt+=idt,{i,n}];
Print[“平均到着時間 =“,avt];(*結果の出力*)
Print[“平均サービス時間 =“,ast];
Print[“システムの全経過時間=“,tt];
Print[“平均待ち時間 =“,N[twt/n]];
Print[“平均空き時間 =“,N[tidt/n]] ];
singleserver[5,2,1000](*関数の実行*)
平均到着時間 =5
平均サービス時間 =2
システムの全経過時間=5258.
平均待ち時間 =0.85806
平均空き時間 =3.33699
3 一般的な待ち行列
3.1 M/M/1(N)
M/M/1に待ち行列をN人までしか許容しないような制約を付けたもので、それ以上に客が来た場合には列に並べず立ち去ることになります。従って、M/M/1の状態遷移がNまでしかない場合と考えることで同様に解くことができます。
k人待ちの状態にある確率は、次式で示されます。

系内の滞在時間は、L=λWの関係から、
平均待ち時間は、Lq=λWqの関係から、求めることができます。
(1)特性値の算定
<<リスト4>>
mm1n[n_,mu_,lambda_]:=
Module[{rou=N[lambda/mu],lq},
lq=N[rou^2*(1-n*rou^(n-1)+(n-1)rou^n)/(1-rou)/(1-rou^(n+1))];
Print[“M/M/1(N)の待ち行列“];
Print[“平均サービス時間=“,lambda];
Print[“平均到着時間 =“,mu];
Print[“待ち行列の許容数=“,n];
Print[“利 用 率 =“,rou];
If[rou>=1,Print[“ρ≧1で計算不能 “];Break,];
Print[“系 内 数 =“,lq/rou];
Print[“行列 の 長さ =“,lq];
Print[“滞 在 時 間 =“,lq/lambda/rou];
Print[“待 ち 時 間 =“,lq/lambda]]
(*平均到着間隔4、平均サービス時間3.5で待ちが最大10人まで系の待ち行列は*)
mm1n[10,4,3.5]
M/M/1(N)の待ち行列
平均サービス時間=3.5
平均到着時間 =4
待ち行列の許容数=10
利 用 率 =0.875
系 内 数 =3.28356
行列 の 長さ =2.87312
滞 在 時 間 =0.938161
待 ち 時 間 =0.820891
(2)シミュレーション
<<リスト5>>
mm1n[v_,s_,t1_,n_]:=
Block[{q1=0,fq=0,t=0,p1=1./v,p2=1./s,a={0} },
While[t<t1,t++;
If[p1>Random[],If[q1<n,q1++,],];
If[p2>Random[],If[q1>0,q1=q1-1,],];
a=Append[a,q1] ];
ListPlot[a,PlotJoined->True]
]
mm1n[4,3.5,1000,10]
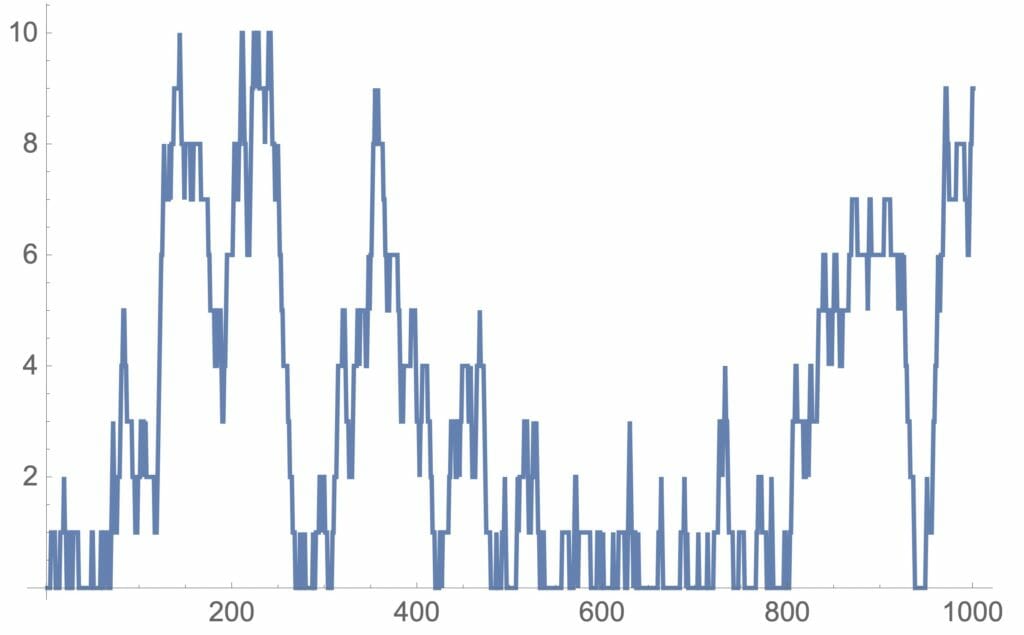
図8:M/M/1(10)のシミュレーション例
上の例では、平均到着間隔4、平均サービス時間3.5で待ち行列は最大10人までしか並べられない場合の例です。
3.2 M/M/s
窓口がs個並列してある場合にもM/M/1と同様の方法で考えることができます。但し、客はs人までは待たされない点には注意する必要があります。
k人待ちの状態にある確率は、a=λ/μ、ρ=a/sと置くと次式で示されます。

(1)特性値の算定
<<リスト6>>
mms[s_,mu_,lambda_]:=
Module[{a,rou,p0,lq},
a=N[lambda/mu];
rou=a/s;
p0=1/(Sum[a^n/n!,{n,0,s-1}]+a^s/(s-1)!/(s-a));
lq=p0*lambda*mu*a^s/(s-1)!/(s*mu-lambda);
Print[“M/M/sの待ち行列“];
Print[“平均サービス時間=“,lambda];
Print[“平均到着時間 =“,mu];
Print[“窓ぐち の 数 =“,s];
Print[“利 用 率 =“,rou];
If[rou>=1,Print[“ρ≧1で計算不能 “];Break,];
Print[“系 内 数 =“,lq+a];
Print[“行列 の 長さ =“,lq];
Print[“滞 在 時 間 =“,lq/lambda+1/mu];
Print[“待 ち 時 間 =“,lq/lambda];
Print[“全窓ぐちが塞る確率=“,p0*mu*a^s/(s-1)!/(s*mu-lambda)]]
(*平均サービス時間12分、平均到着時間5分で窓口が3つの系の待ち行列*)
mms[3,12,5]
M/M/sの待ち行列
平均サービス時間=5
平均到着時間 =12
窓ぐち の 数 =3
利 用 率 =0.138889
系 内 数 =0.462799
行列 の 長さ =0.0461323
滞 在 時 間 =0.0925598
待 ち 時 間 =0.00922645
全窓ぐちが塞る確率=0.00922645
(2)シミュレーション
M/M/sについて、待ち行列の変化だけを見る簡単なシミュレーションを揚げておきます。
<<リスト7>>
mms[v_,s_,t1_,c_]:=
Module[{que=0,t=0,p1=1./v,p2=1./s,a={0},srv,i,total},
Do[srv[i]=0,{i,1,c}];
While[t<t1,t++; If[p1>Random[],que++,];i=1;
While[i<=c, If[srv[i]==0, If[que>0,que–;srv[i]=1,],
If[p2>Random[],If[que>0,que–,srv[i]=0],];
];
i++;];
total=0;
Do[total=total+srv[i],{i,1,c}];
AppendTo[a,que+total];];
ListPlot[a,PlotJoined->True]];
mms[5,12,300,3]
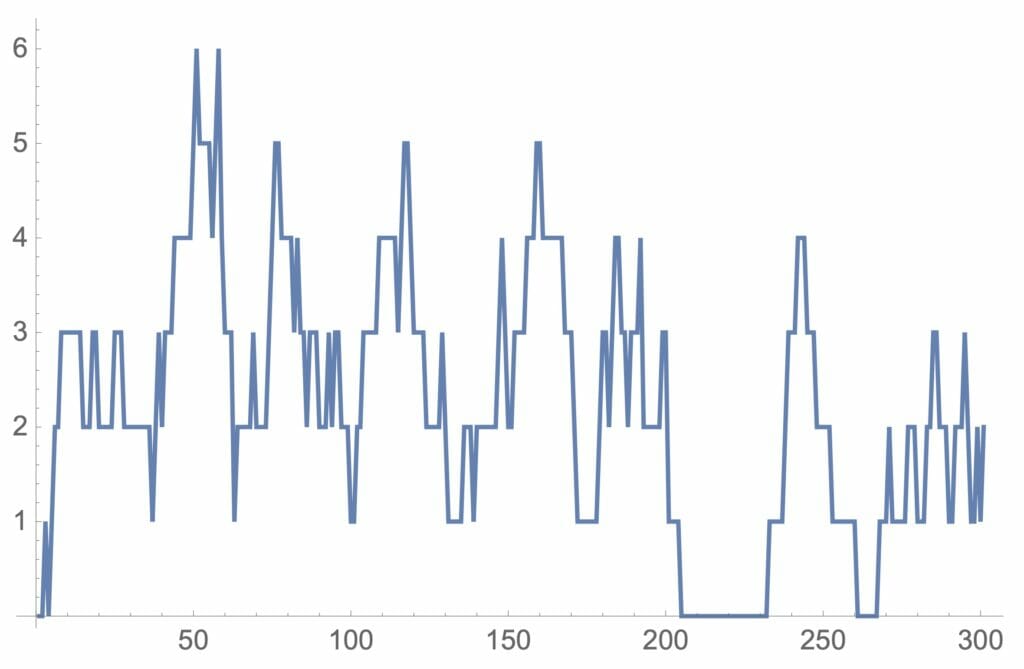
図9:M/M/Sのシミュレーション例(窓口が3つある場合)
上の例では、平均到着間隔5、平均サービス時間12で窓口が3つある場合の例であり、サービスを受けている人も含めているので待ち行列が3以下の場合は待ちがないことになります。
ここで、窓口を4つにするとmms[5,12,300,4]でシミュレーションできます。
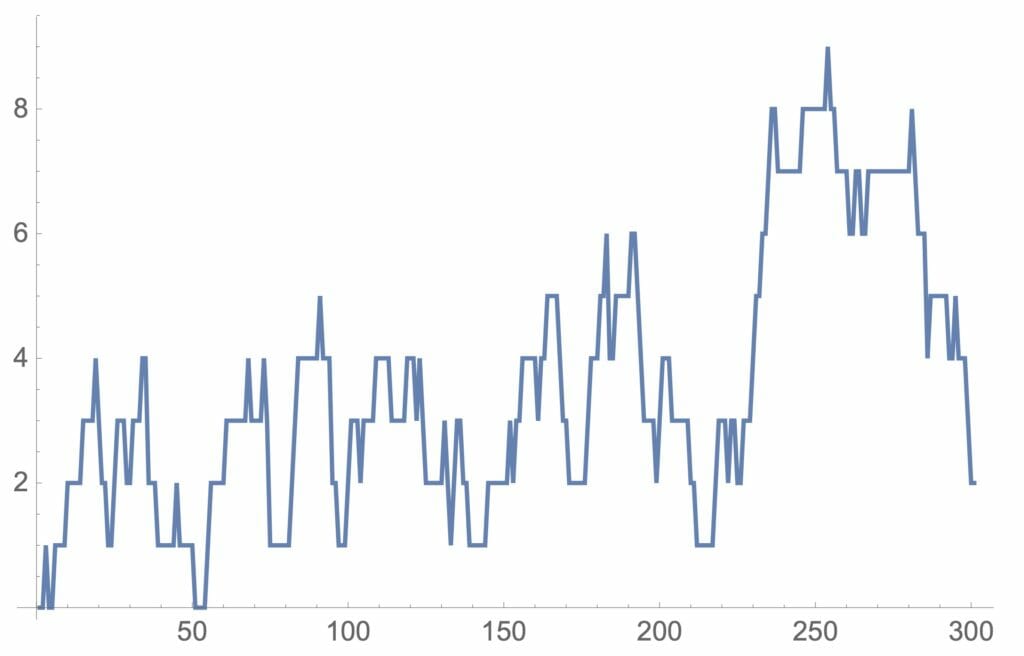
図10:M/M/Sのシミュレーション例(窓口が4つある場合)
4以下の場合が多く、窓口が空いた状態になっていることがわかります。客としてはこのくらい余裕が欲しいものです。
4 応用例
これまでの例は、平均到着時間と平均サービス時間がともに一定でしたが、実際の場合には時間毎に変化するものです。例えば、駅の新聞売りの平均到着時間は、朝のラッシュ時が最大のピークであり、夕方は夕刊を買う人が小さなピークを作ると予想されます。このときの待ち行列がどうなるかを考えてみましょう。
このように平均到着時間が変化する場合は、これまでに述べた特性値を計算しても、その時その時の値であり、あまり意味がありません。このような時は大ざっぱに待ち行列の変化が目に見えたほうが分かり易いでしょう。
シナリオとして次のようなことを考えてみます。ある店では、平均サービス時間は3分で一定ですが、客の到着の平均は次のように変化する。開店の6時には、まだ客は少なく25分に1人位ですが、8時には、2分に一人となり、12時には少なくなり15分に1人となります。4時にまた小さなピークを迎え5分に1人となるが閉店時の6時には20分に1人になってしまう。
まず、リスト8では、上のシナリオで上げた数字を関数で近似し、図11に近似した関数を図示して確かめてみています。なお、横軸の時間は、開店の朝6時を0として分単位で取っています。従って、閉店の夕方6時は、12時間=720分で示されています。
<<リスト8>>
a={{0,25},{120,2},{360,15},{600,5},{720,20}};(*近似したいデータ*)
avt[x_]=Fit[a,{1,x,x^2,x^3,x^4},x];(*近似式の取り出し*)
Plot[avt[x],{x,0,720}](*近似式の作図*)
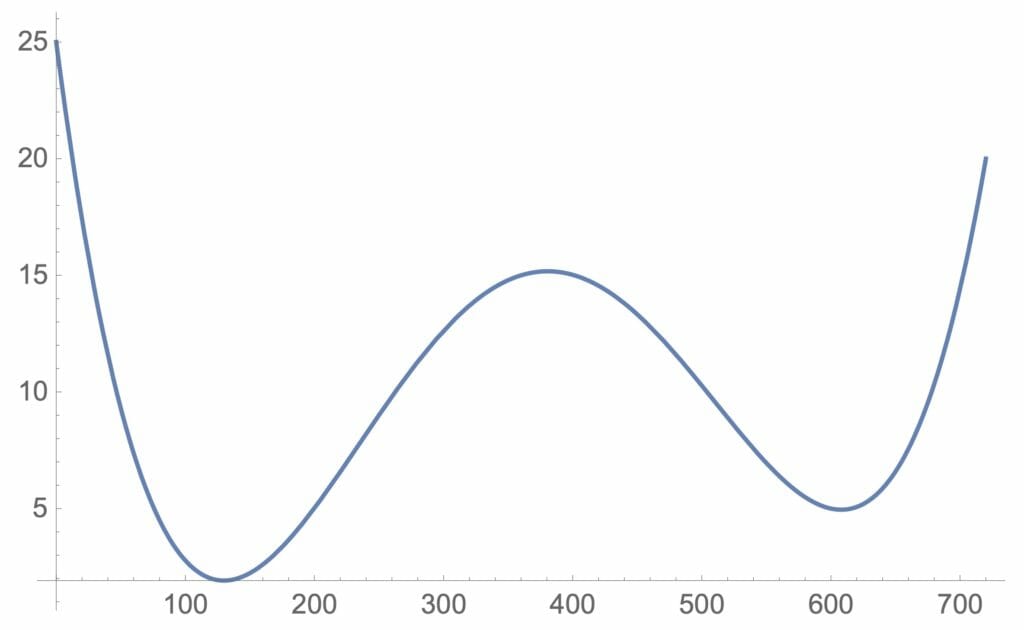
図11:近似した関数
次にリスト9は、平均到着時間を関数で表せるように改良したものです。図12にシミュレーションの結果を示しました。図12を見ると朝のピーク時の100分後(7時50分)から250分後(10時10分)までは、15人程度の待ち行列がたえずできているのが分かります。その他は、散発的に短い待ち行列ができるだけであり、夕方のピークについてもほとんど関係ないことが分かります。
<<リスト9>>
mm1vv[s_,t1_]:=(*関数の定義*)
Module[{q1=0,fq=0,t=0,p2=1./s,a={0} },(*変数の定義*)
While[t<t1,t++;(*t1まで続ける*)
If[1/avt[t]>Random[],q1++,];(*来客*)
If[q1>0 && p2>Random[],q1=q1-1,];(*サービス*)
AppendTo[a,q1] ];(*リストへ出力*)
ListPlot[a,PlotJoined ->True](*作図*)
];
mm1vv[3,720](*関数の実行*)
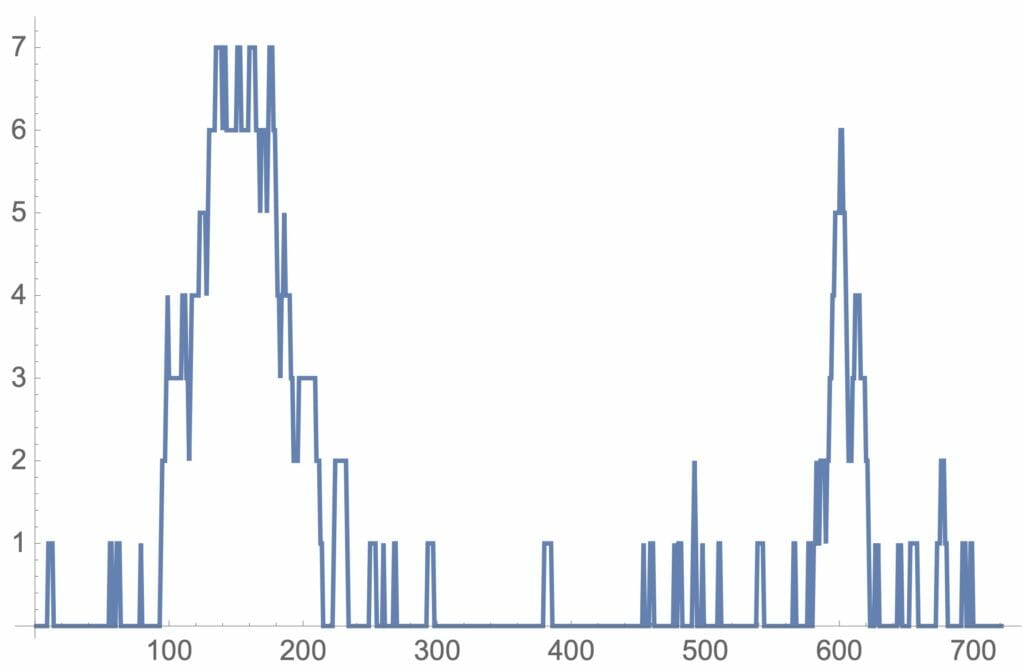
図12:平均到着時間が変化したときの待ち行列の変化
平均サービス時間を変化させた場合、例えば午前中だけパートの人を雇うことで、平均サービス時間を短くできた場合等のシミュレーションについても、先ほどの例とほぼ同様に改良することができます。
8時から10時までに10人以上の待ち行列ができ、処理できないことが予想されるので、この時間だけパートを雇った場合について考えてみましょう。この場合、正確にはM/M/sの場合が良いようですが、実際には2つの待ち行列ができるので到着時間間隔が2倍になったと考えて良いでしょう。従って、平均サービス時間を変化させなくても到着時間間隔を変化させることで対応できます。
<<リスト10>>
a={{0,25},{120,4},{360,15},{600,5},{720,20}};(*近似したいデータ*)
avt[x_]=Fit[a,{1,x,x^2,x^3,x^4},x];(*近似式の取り出し*)
Plot[avt[x],{x,0,720}](*近似式の作図*)
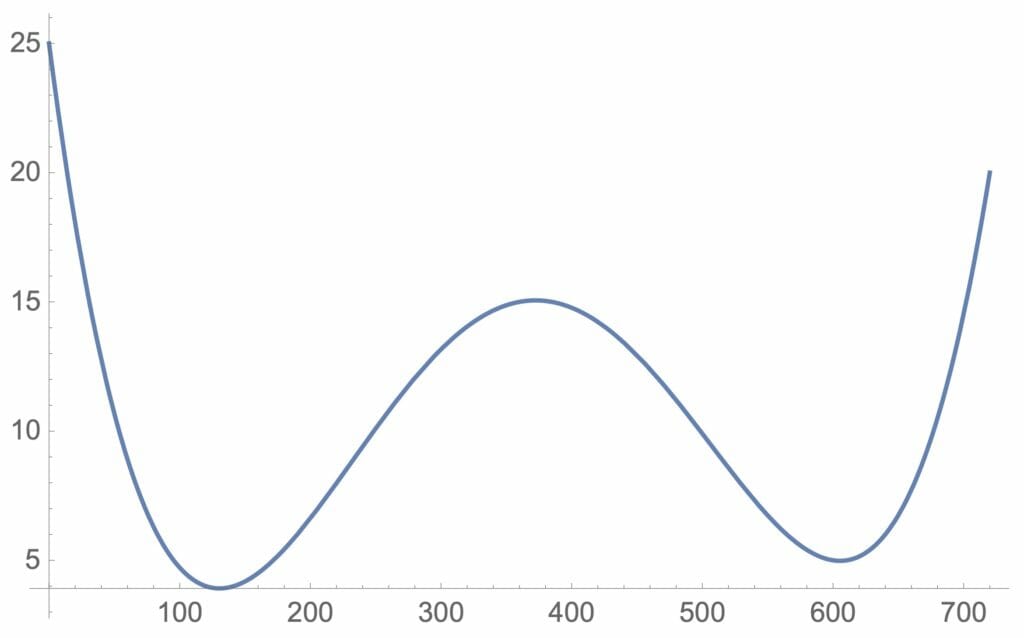
図13:近似した到着時間間隔(パートを雇った場合)
この到着時間間隔に従ってもう一度待ち行列の変化をみてみるために、リスト9を再度実行すると図14を得る。
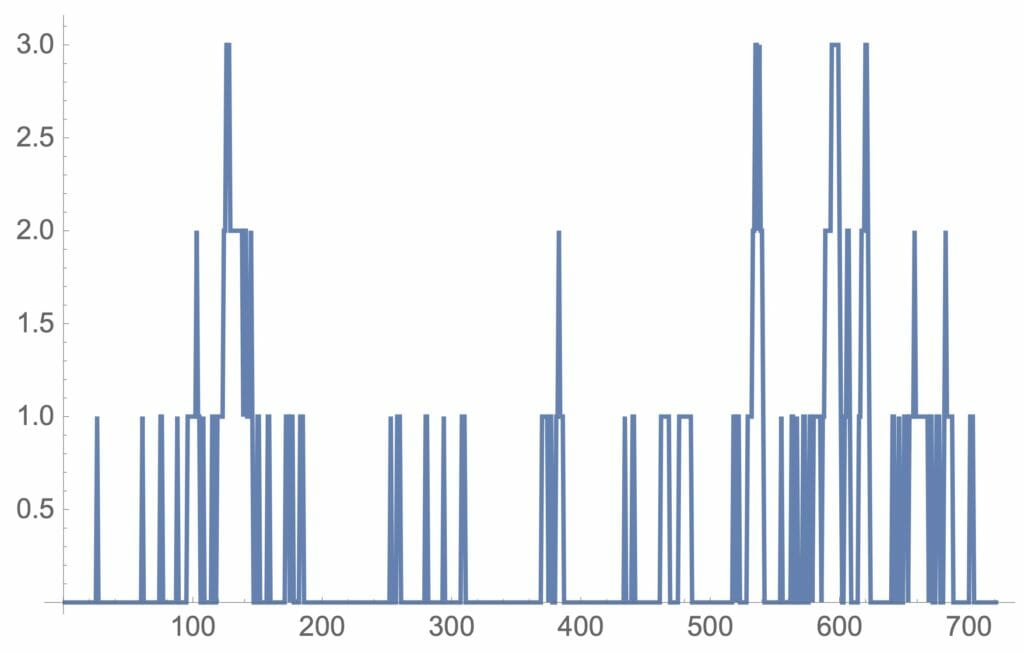
図14:待ち行列の大きさ(パートを雇った場合)
パートを雇った効果により、待ち行列は最大でも3名と無理な待ち行列は解消されています。
参考文献
1 森村・大前OR ライブラリー 13「待ち行列の理論と実際」日科技連
2 中村健蔵2019『MathematicaによるOR』楽天Kobo・キンドルDP
ノートブックのダウンロードについて
ノートブックを下からダウンロードのページへ行き、ダウンロードできます。但し、ダウンロードのページに入るには、下で問い合わせて、メールしで送られて来るパスワードが必要です。なお、ダウンロードのページでノートブック全てが管理されています。つまり、1度メールを送れば、その他の記事のノートブックもダウンロード出来ます。さらに新しい記事をアップロードした際にお知らせいたします。また、ノートブックは配布可能ですので、Mathematicaを使っている友人等で興味のある方に配布して下さい。
パスワードが必要な方は、下の問い合わせからメールをお送りください。
なお、新しい記事をアップロードした際にお知らせいたします。また、お名前、メールアドレスはサーバーに残さず、管理していますので、ご安心ください。