要旨:今回はインターネットで新しい幾何学キルトの潮流を見つけ、元になっている幾何学等を解説しながらご紹介します。
幾何学からの動き
まず、本連載第3回でも、ご紹介した1種類でタイリングできる15番目の五角形に関する2015年の大発見については、ニット作品しかを見つけることはできませんでした。この五角形はお世辞にも目を引くような形とは言えない上に、12個が1つの塊となって繰り返しの単位となっている特徴のために、なかなかキルト等には難しいようです。ちょっと強引ですが、筆者が竹垣を支えにしたサボテンの花をイメージしたデザインが図1です。

図1:新発見の五角形で構成したデザイン例
サボテンの花ならどうにかありかな?というところでしょうか。さて、このデザインでキルトを作成すれば、世界で初めてのキルトとなります。作成してみたい方は編集部までご連絡ください。
ペンローズ・タイリング
昔から非周期的なタイリングができないかという興味があり、挑戦されていましたが、イギリスの数理物理学者であるロジャー・ペンローズ博士が2個の図形で5回の回転対象性を持つ非周期的なタイリングできるものを1970年代に見つけました。なお、それ以降も1種類でできるものは見つかっていません。また、1984年に5回の回転対象性を持つ非周期的な構造の準結晶と呼ばれる物質が見つかり、ペンローズ・タイリングが存在を予言し、理論的な説明を与えるものとして話題になりました。準結晶についての説明は省略しますが、ペンローズ・タイリング自体が美しく、興味深い構造を持っているので、その点について説明します。

図2:ペンローズ・タイリングの基本図形(P2:矢じりと凧)
図2左図はペンローズ・タイリングの基本となる矢じりと凧と呼ばれる2つの形で、数字は角度です。中央図は基本の2つの形を使って周期的な配列をしたもので、右図は非周期配列の一例です。ただし、この基本形は改良されて、図3になりました。なお、図3の構成自体は、拡張していっても非周期になるものではありません
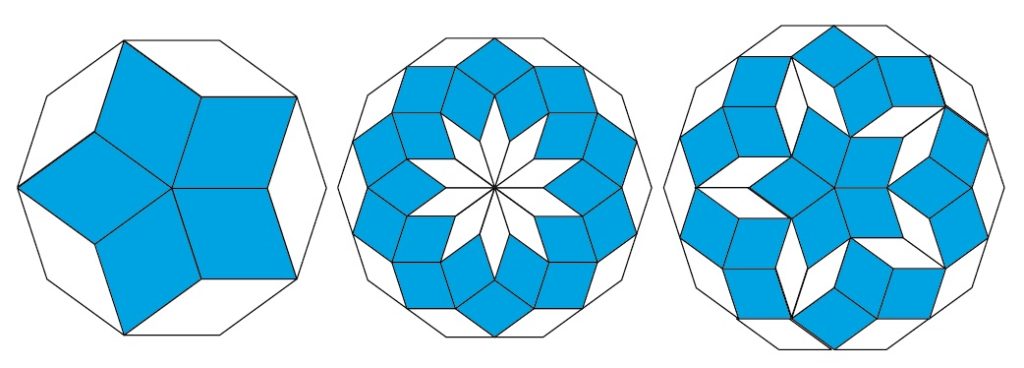
図3:ペンローズ・タイリングによる外形が正十角形の構成
改良された基本形は白の細い菱形と青の太い菱形です。図3は2つの菱形を使って、外形が正十角形になるように構成したものです。さて、図3中央図を見て、どこかで見たと思われた方は記憶抜群です。前回、正十角形10個を各頂点1箇所で重ねて構成した正十角形です。筆者が少年時代に図形を描いて遊んでいた時に準結晶のヒントがあったなどとは思いも寄りませんでした。

図4:ペンローズ・タイリングを応用したキルト
図4はペンローズ・タイリングを応用したドイツのCorinna Beuermann-Kulpさんのキルトで、大きさは227cm x 183cm、8ヶ月をかけてマーティン・ルーサーの宗教改革500周年を記念して作成されたキルトで、ルーサーのバラをデザインに取り入れたものです。下のボタンを押せば、Corinna Beuermann-Kulpさんの沢山のキルトを見ることができます。
フラクタル
フラクタルは1975年頃に提唱された「宇宙・自然は入れ子構造である。」という幾何学概念であったために美術をはじめ広い分野に影響を与えており、キルトの中にもこれらを取り込んだものが出てきています。
まずはフラクタルに関する解説を行い、関連するキルト作品を紹介します。
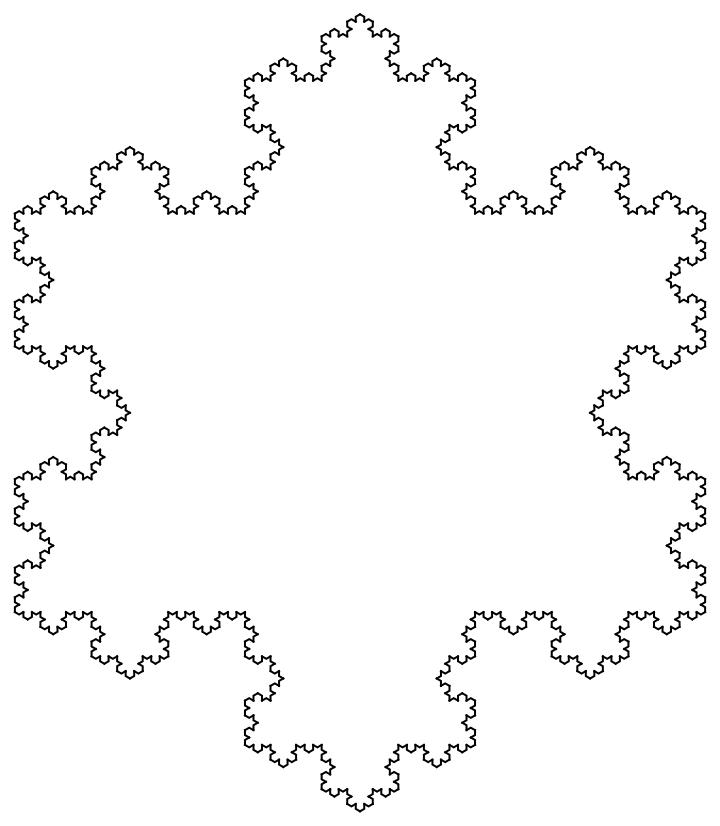
図5:フラクタルの一例
図5左図はロマネスコと呼ばれるカリフラワーの1種で、最近はスーパーでも見かけるようになりました。一部分を取ってみると全体と同じ形をしている性質(自己相似性)が自然界に見られる典型的な入れ子構造として有名です。右図は雪片曲線と呼ばれるフラクタル図形で外周の長さが無限大という常識では考えられないものとなっています。参考文献1第4章に代表的なフラクタル図形や非整数の次元について解説しています。ちなみに雪片曲線の次元は1.26と整数ではありません。ご参照下さい。
図6:フラクタルに関連するキルト
図6左図は雪片曲線キルトの大きさは1m四方で、大小を重ねたり、外側に配置されており、背景の暗さもあり、雪降る夜に大きな雪の結晶を見つけたというイメージでしょうか。
右図は「シダの葉」という題名で、ジュリア集合と呼ばれるフラクタル図形をシダの葉に見立てて制作されたものです。大きさは35cm✖️25cmで、作成した図形を布へインクジェット印刷し、刺繍を加えたものです。
作成者はいずれもブログで自分の作品を掲載しており、そのURLを表示していますので、興味のある方はご参照ください。フラクタルでは自己相似性を表現するため、細かい部分を緻密にする必要があり、いずれも労作です。
※シダの葉の作者のWebページは2020年3月9日現在、見ることが出来ませんでした。
だまし絵(トロンプ・ルイユ)からの潮流
15年ほど前から日本では動く錯視が流行していますが、はるか昔からだまし絵とよばれるものがあり、シュールレアリズムやオプ・アート(光学的芸術)、トリック・アート等、時代的な流行を反映させながら変化してきた潮流があります。一言で言ってしまえば、人を驚かせたいという遊び心の所作と言ってもいいかもしれません。参考文献2は筆者が錯視の項目について執筆協力していますので、ご参照下さい。
図7:だまし絵関連のキルト(迷路、オプ・アート、動く錯視)
図7は、だまし絵に関連するキルトです。左図は迷路キルトとも呼ばれているもので、まさに立体的な迷路がベッド上に展開されています。中央図は典型的なオプ・アートの図案で、中央が盛り上がって見えるように設計されたデザインです。なお、この2点の図案は欧米ではキットが販売されているように典型的なものです。右図は動く錯視のキルトで、動いて見える人には螺旋状に回転しているように感じらます。なお、2割程度動いて見えない方もいらっしゃいますので、ご安心ください。米国の方が作ったものでブログのURLを表示しています。題名は「捻れたログキャビン」で、大きさは70cm四方です。
日本では和のキルトの創造という潮流
最後に日本では和のキルトの創造という潮流が見られます。ただし、その定義はなく、作家さんがそれぞれ思うところを表現しているようです。色々ありますが、和の幾何学キルトとなると、伝統の幾何学文様を取り入れた図9のようなものになるのではないでしょうか?

図8:和の幾何学キルト
図8は昨年のキルト&ステッチ展大阪にあった勝又今日子さんの作品で七宝つなぎの花模様と尖った三角形、さらに分割した三角形でタイトル通りの「布あそび」を楽しんでいる様が感じられました。
なお、筆者は和の幾何学キルトには、やはり一応の定義が必要ではないかと考えます。たとえば、「和の幾何学キルトとは、日本伝統の幾何学文様を取り入れ、さらなる革新を目指すもの」という定義は如何でしょうか?筆者としても日本伝統の幾何学文様の革新を目指してデザインをしていきたいと考えております。
まとめ
以上で第7回は終了です。幾何学キルトの世界的な潮流に目を向けてみました。人間の根本的な好奇心に基づくもの、1975年に提唱された理論に基づくものなど、新旧大小のトレンドが見えてきました。
さて、次回第8回はとりあえず、連載の最終回です。これまで幾何学デザインを出来るだけ平易に解説してきましたが、やはり、制約が大きいと感じられていることと思います。 最終回は「幾何学デザインをもっと楽しく」と題して、幾何学デザインの自由度を上げるお話をさせていただき、多角形がメタモスフォーゼ(変容)していくキルトデザインに挑戦します。ご期待ください。
参考文献
1 中村健蔵1998年『Mathematicaで絵を描こう』東京電機大学出版局
2 形の科学会編集2011年『かたち・機能のデザイン事典』丸善(株)
3 中村健蔵2019『パッチワークキルターのための幾何学デザインシリーズ 基礎編 幾何学で進化するキルトデザイン』キンドルDP