要旨:正多角形でない一般図形によるタイリングについて解説します。
正多角形でない一般図形によるタイリング
これまで正多角形が1種類の場合、2種類以上の場合とまどろっこしい説明だと思われたかもしれません。まず特別な場合を考え、その条件を緩和していくことで、より一般的なことに応用していくことを考えていこうというものです。
それでは、1種類の一般図形によるタイリング、つまり、ある形があった場合、その形だけで平面を隙間無く埋めることができるかどうかについて、まとめます。その説明図を図1に示します。黒塗りが1つの図形です。

図1:一般図形によるタイリングの説明
① 四角形と六角形は対辺が平行で等しい長さの平行四辺形と平行六辺形はタイリングできます。
② 三角形と四角形ですが、どんな三角形でも、どんな四角形(凹図形を含む)でも、タイリングできます。これは、それぞれ2つを合わせると平行四辺形、平行六辺形を作ることができることから解ります。
③ 五角形については特殊な条件の15種類でタイリングできることが知られています。なお、15番目は2015年に見つかり、これ以上ないことを証明したとしていますが、30年前に14番目が見つかった時も、これ以上ないことを証明したとしていましたので、16番目が存在する可能性は十分にあると期待しています。五角形については利用できそうな幾つかについて後ほど説明します。
④ その他、凸図形については、平行六辺形以外の六角形と7角形以上のタイリングはできません。逆に五角形以上の凹図形や曲線を含む図形はタイリングできるものが多くあります。そして、それには特別な条件はありません。これは、五角形以上の凹図形や曲線を含む図形がタイリングできるという意味ではなく、出来るかどうかを試行錯誤で確認しなければならないという意味です。
プログラムを含む色々な作り方が図1右図のように考案されており、挑戦することができます。なお、2種類以上の図形によるタイリングについては、答えが多すぎて定まりません。例えば、図1右図上部のようにタイリングできる図形を2つに分割した場合、当然ですが2つ合わせればタイリングできる図形になります。分割方法に特別な条件はなく、これだけで無限の種類を作ることができることになります。従って、例えば、「凸な五角形2種類を使って」といった条件をつけない限り、答えが無限に存在し、意味のないものになってしまいます。
以上が一般図形のタイリングについてまとめたものです。
さて、一般図形のタイリングの応用法としては、好きな形がタイリングできるかを確認して、できるのであれば、それを敷き詰めたものでデザインしてみれば良いわけです。例えば、三角形や四角形はどんな形でもタイリングできるわけですから好きな三角形や四角形を選ぶことができます。後ほど、あとの説明も加味して図案例を説明します。ただし、好きな三角形や四角形といわれてもなかなか思い浮かばないかも知れません。
直角二等辺三角形の利用
応用についてのもう1つの考え方として、これまで親しんできた正方格子(正方形を敷き詰めたもの)や六方格子(正三角形を敷き詰めいたもの)の中で使いやすい図形でバリエーションを増やして行くというものです。
まず、正方格子から考えて見ましょう。正方形以外で基本的な図形として使えそうなものとしては直角二等辺三角形があります。正方形を対辺で2分割したもので、三角定規として使い、懐かしい方も多いと思います。図2に正方形を直角二等辺三角形に32分割した2種類を作り、色付けました。2種類は分割の方向が異なり、デザインにバリエーションをつけることができます。

図2:正方格子への直角二等辺三角形の導入
さて、正方形以外で基本的な図形として直角二等辺三角形を考えた時、正八角形の内部分割を考えることができます。

図3:正八角形の内部分割
図3に3つの図を挙げています。左図は正方形から4つの黒い直角二等辺三角形を切り取ることで正八角形が出来る事が解ります。つまり、これにより正方格子の中にデザインとして正八角形を取り入れることができます。
中央図では、正八角形の中を正八角形と直角二等辺三角形に分割しています。
さらに右図では中央図の直角二等辺三角形を半分の面積の直角二等辺三角形に分割してあります。なお、これらは花をイメージして色付けを行いました。参考文献1やインターネット上で調べても正八角形に基づくデザインは少なく、私は勝手に扶桑日輪と名付けました。マリナーズコンパスにも劣らないシンプルで強い構成であると思うのですが、如何でしょうか?
次に正方格子で利用できる五角形について説明します。五角形は不思議な形で、立体ではサッカーボールのように正五角形も活躍しているのですが、平面ではなかなか活躍の場がありません。図4は正方格子で利用できる五角形とそれを用いたデザイン例です。5個の正方形から直角二等辺三角形を利用することで4個の五角形を作ることができます。また、正八角形を4分割するとダイヤモンドの五角形になります。アクセントとして利用すれば、正方格子のバリエーションを増やすことができることがお分かりいただけると思います。

図4:正方格子で使いやすい五角形
図5は正八角形を含むアルキメデスタイリングの図案を正八角形と直角二等辺三角形に分割しました。なお、中央の正八角形はさらに内部分割しています。また、色付けの方では2種類の五角形を入れました、バリエーションとして如何でしょうか?
ところで、正八角形を含むタイリングは正方格子と連接できるのかというと直角二等辺三角形をうまく使うことで、デザイン的には問題なく連接できます。しかしながら、内部分割をしたら頂点が微妙にずれてしまいます。

図5:正八角形を含むアルキメデスタイリングの内部分割
普通の三角形を使ったデザイン

図6:普通の三角形を使ったデザイン例
図6は普通の三角形を使ったデザイン例として縦横3対1の縦長の直角三角形を使用したものです。それだけでは思ったように表現できませんでしたので、縦横1対1の直角二等辺三角形、つまり、3つ縦に重ねて連接し、大木と吹き渡る風というイメージを表現してみました。
六方格子を使ったデザイン
次に六方格子について考えます。基本的な図形として、正三角形を2つ合わせた菱形はシンプルで強い形であると思います。これを組み合わせた三菱や六角星などとして使えるのではないでしょうか?また、この菱形を縦方向に2等分した頂角120度を持つ二等辺三角形も面白いと思います。日本の伝統模様で言えば麻の葉の基本となるものです。
図7にそれらとデザイン例を示しました。構成イメージは「下からすくすくと伸びた葉っぱは、上の方でいっぱいに光を受け止める。やがて蕾ができ、花がほころび始める。そして、大輪の花ぐるまが咲く!」で如何でしょうか?

図7:六方格子への菱形の導入
また、図8に六方格子で使いやすい五角形を示しました。正六角形を2等分、3等分したものや正六角形に正三角形をつけたものなど、いろいろなものがあります。黒塗りが1つのピースで、2つ、もしくは3つを合わせると平行六辺形になりますので、タイリングできることが分かります。さらにそれらを使ったデザイン例を示しました。構成イメージは、「色々な草が生い茂り、花が咲く。蝉やてんとう虫なども活発に活動している!」です。狭い中に詰め込んだので、ごたごた感がありますが、六方格子のバリエーションが広がったと感じていただければ、嬉しい限りです。
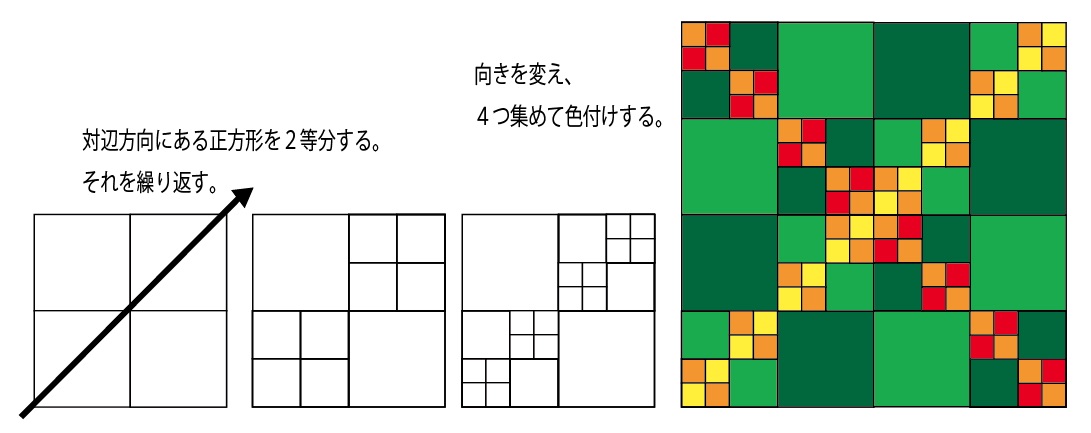
図8:六方格子で使いやすい五角形
以上で第3回の説明は終了です。
まとめ
第3回では、一般図形のタイリングについて説明しました。タイリングは思っていたよりも自由な世界で、どんな三角形や四角形もタイリングできます。しかしながら、自分の好きな三角形や四角形のタイリングだけで自分のイメージを表現することは難しいものと思われます。従いまして、筆者としては、色々なバリエーションを持つことができる正方格子や六方格子の中で利用できるシンプルで強く美しい形をご紹介し、イメージに合うものや好きな形に近いものを見いだしていただければと考えます。菱形の美しさや五角形の面白さを感じていただけたのであれば、筆者の喜びとするところです。
次回はこれまで簡単な説明しかしていなかった内部分割をする時のルールや規則について説明します。幾何学的なフレーバーを感じて頂けるように努力しておりますので、ご期待ください。
ところで本年12月、筆者在住近傍の長崎県立美術館で個展が開かれます。本誌、イベント・カレンダーをご参照ください。
参考文献
1 中嶋由美子2015年「パッチワークパターン集1050」パッチワーク通信社
2 中村健蔵2019『パッチワークキルターのための幾何学デザインシリーズ 幾何学で進化するキルトデザイン』楽天Kobo・キンドルDP


